Notes on Integer/Float Operations

一些整数和浮点数的基础，最近碰到一些坑，顺手整理一下。有的章节写的不太细是因为手头上没碰到直接的坑，所以只收集材料，不过多展开。碰到再补上。

整数的表示

https://blog.mwish.me/2020/09/19/Integer-Endian/

本节图片来自：https://cs61c.org/sp25/lectures/lec02/

对于无符号整数 (unsigned integer)，所有操作正如最简单的想象。Unsigned Number 的 overflow / underflow 是良定义的：

img

对于有符号数字，这里关注：https://en.wikipedia.org/wiki/Two's_complement#Arithmetic_operations

这里关注到 One’s complement （第一位表示符号位，会有 -0）和 Two’s complementy

img

这里具体操作中，实际上 signed overflow/underflow 实际上是 ub: https://en.cppreference.com/w/cpp/language/ub

这里也有帖子讨论：https://stackoverflow.com/questions/70801443/why-is-signed-overflow-due-to-computation-still-undefined-behavior-in-c20

  1. 不一定真的是二进制补码实现的整数
  2. 这里有一些优化问题，会导致实现出现问题

这里的含义其实是，signed integer overflow只是在 C/C++ 里是UB，更低层面实际可能大部分平台是有良好定义的。

safe_math

我们假设有一个特别简单的需求，实现 delta 编码，(假设) 这个地方编码是一个 int32_t domain。然后会有两个值: int32_t::min(), int32_t::max(), int32_t::min()，这个很正常。然后我们就会（很轻松的发现）这两个数字的差值无法用 int32_t 表示，需要用 uint32_t 表示。

那么这个地方 int32_t v = cur - last 实际上就可能导致 overflow/underflow 的 ub 了。 但实际上它们的差值可以用 32 位表示出来。这里关注 arrow 的实现，里面加了一个 SafeSignedSubtract，因为这套操作在 unsigned 上并不是 ub

1
2
3
4
5
6
7
/// Signed subtraction with well-defined behaviour on overflow (as unsigned)
template <typename SignedInt>
SignedInt SafeSignedSubtract(SignedInt u, SignedInt v) {
  using UnsignedInt = typename std::make_unsigned<SignedInt>::type;
  return static_cast<SignedInt>(static_cast<UnsignedInt>(u) -
                                static_cast<UnsignedInt>(v));
}

那么我们假设运行下列代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <vector>

template <typename SignedInt>
SignedInt SafeSignedSubtract(SignedInt u, SignedInt v) {
  using UnsignedInt = typename std::make_unsigned<SignedInt>::type;
  return static_cast<SignedInt>(static_cast<UnsignedInt>(u) -
                                static_cast<UnsignedInt>(v));
}

int main() {
  using T = int32_t;
  std::vector<T> int_values = {std::numeric_limits<T>::min(),
                               std::numeric_limits<T>::max(),
                               std::numeric_limits<T>::min(),
                               std::numeric_limits<T>::max(),
                               0,
                               -1,
                               0,
                               1,
                               -1,
                               1};
  for (size_t i = 0; i < int_values.size(); i += 1) {
    T u = int_values[i];
    T v = int_values[i + 1];
    T result = SafeSignedSubtract(v, u);

    std::cout << "SafeSignedSubtract(" << v << ", " << u << ") = " << result
              << ", unsigned: "
              << static_cast<typename std::make_unsigned<T>::type>(result)
              << '\n';
  }
  return 0;
}

可以得到结果：

1
2
3
4
5
6
7
8
9
10
SafeSignedSubtract(2147483647, -2147483648) = -1, unsigned: 4294967295
SafeSignedSubtract(-2147483648, 2147483647) = 1, unsigned: 1
SafeSignedSubtract(2147483647, -2147483648) = -1, unsigned: 4294967295
SafeSignedSubtract(0, 2147483647) = -2147483647, unsigned: 2147483649
SafeSignedSubtract(-1, 0) = -1, unsigned: 4294967295
SafeSignedSubtract(0, -1) = 1, unsigned: 1
SafeSignedSubtract(1, 0) = 1, unsigned: 1
SafeSignedSubtract(-1, 1) = -2, unsigned: 4294967294
SafeSignedSubtract(1, -1) = 2, unsigned: 2
SafeSignedSubtract(0, 1) = -1, unsigned: 4294967295

对于 int32_t::min(), int32_t::max(), int32_t::min() 序列，第一个是 uint32_t::max 很好理解，但是第二个是 1，为什么不应该是 -int64_t(uint32_t::max()) 呢（当然，这里无法用 32 bit 表示），为什么 -2147483648 - 2147483647 是 unsigned: 1 呢？往上翻翻 011111..111 + 1 之后就是 10000...000 了！这里实际上很巧妙用这套操作回绕了。

这里在指令上会有区别吗：https://godbolt.org/z/MjEh3zKsT 答案是：现在还没有。这个地方是不是很有趣？利用这个回环来处理 delta。不过还没完，我们可以看到这个 Patch: https://github.com/apache/arrow/pull/37940/ . 这里讲到，诶 -1 - 1 = -2 = (unsigned) 4294967294 然后存 unsigned bits 太变态了，我们还是做一些优化吧。这个 patch 也比较有意思，看下来应该能成为 Signed 大师。

实际上，gcc 还提供了一些 builtin: https://gcc.gnu.org/onlinedocs/gcc/Integer-Overflow-Builtins.html

1
2
3
4
5
6
7
8
int32_t sub5(int32_t v1, int32_t v2) {
    int32_t v ;
    bool res = __builtin_sub_overflow(v1, v2, &v);
    if (res) {
        return 0;
    }
    return v;
}

这里汇编可能会是:

1
2
3
4
5
6
7
8
sub5(int, int):
        sub     edi, esi
        jo      .L8
        mov     eax, edi
        ret
.L8:
        xor     eax, eax
        ret

一些汇编操作 Notes

我们回顾一下 x86 汇编：

  • 有符号整数和无符号整数的加减都是 add sub
  • 乘法 除法有有无符号的区分，可以是 imul mul idiv div，结果可以保留到两个寄存器中

参考 Table: https://www.cs.cmu.edu/afs/cs/academic/class/15213-f09/www/misc/asm64-handout.pdf

img

img

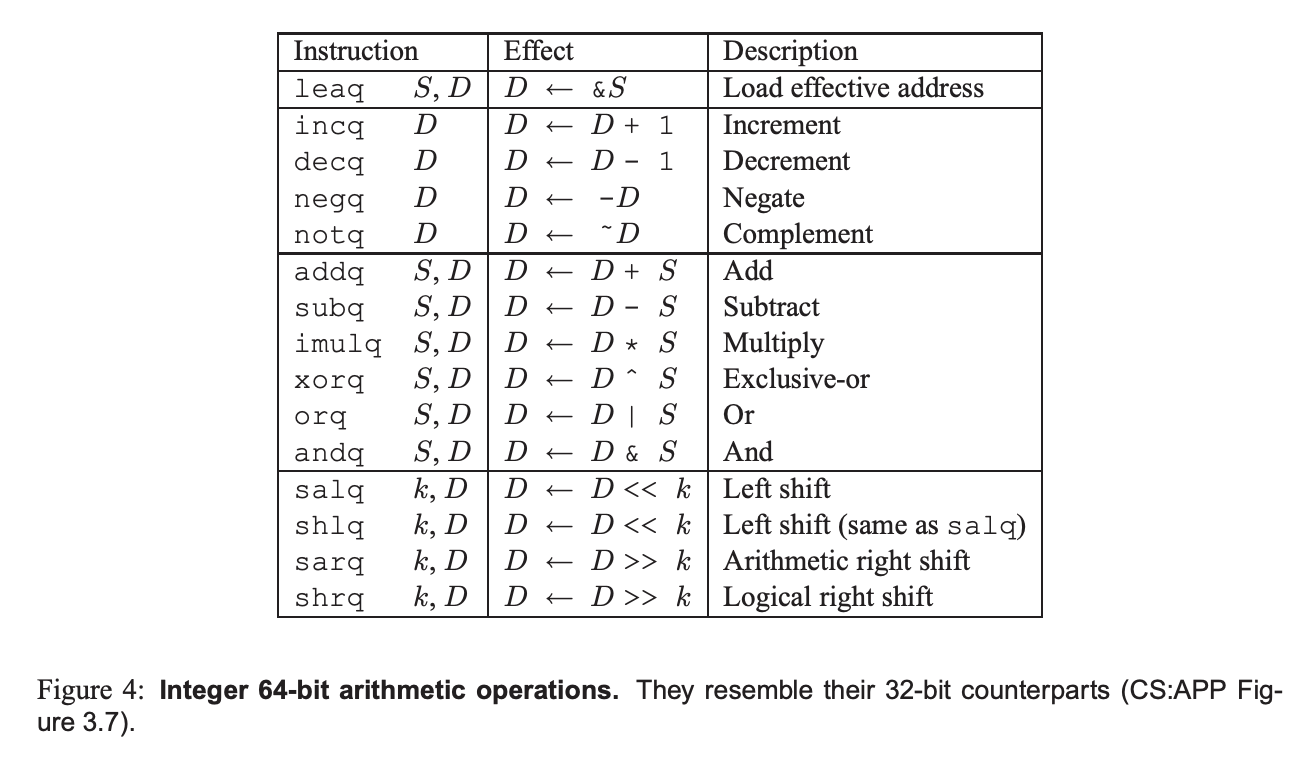
这里可以再次复习区分一下有符号和无符号的 shift:

  1. https://en.wikipedia.org/wiki/Arithmetic_shift
  2. https://en.wikipedia.org/wiki/Logical_shift
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/*
shift1(int, int):
        mov     eax, edi
        mov     ecx, esi
        sar     eax, cl
        ret
shift2(unsigned int, int):
        mov     eax, edi
        mov     ecx, esi
        shr     eax, cl
        ret
*/
int32_t shift1(int32_t v1, int32_t v2) {
    return v1 >> v2;
}

uint32_t shift2(uint32_t v1, int32_t v2) {
    return v1 >> v2;
}

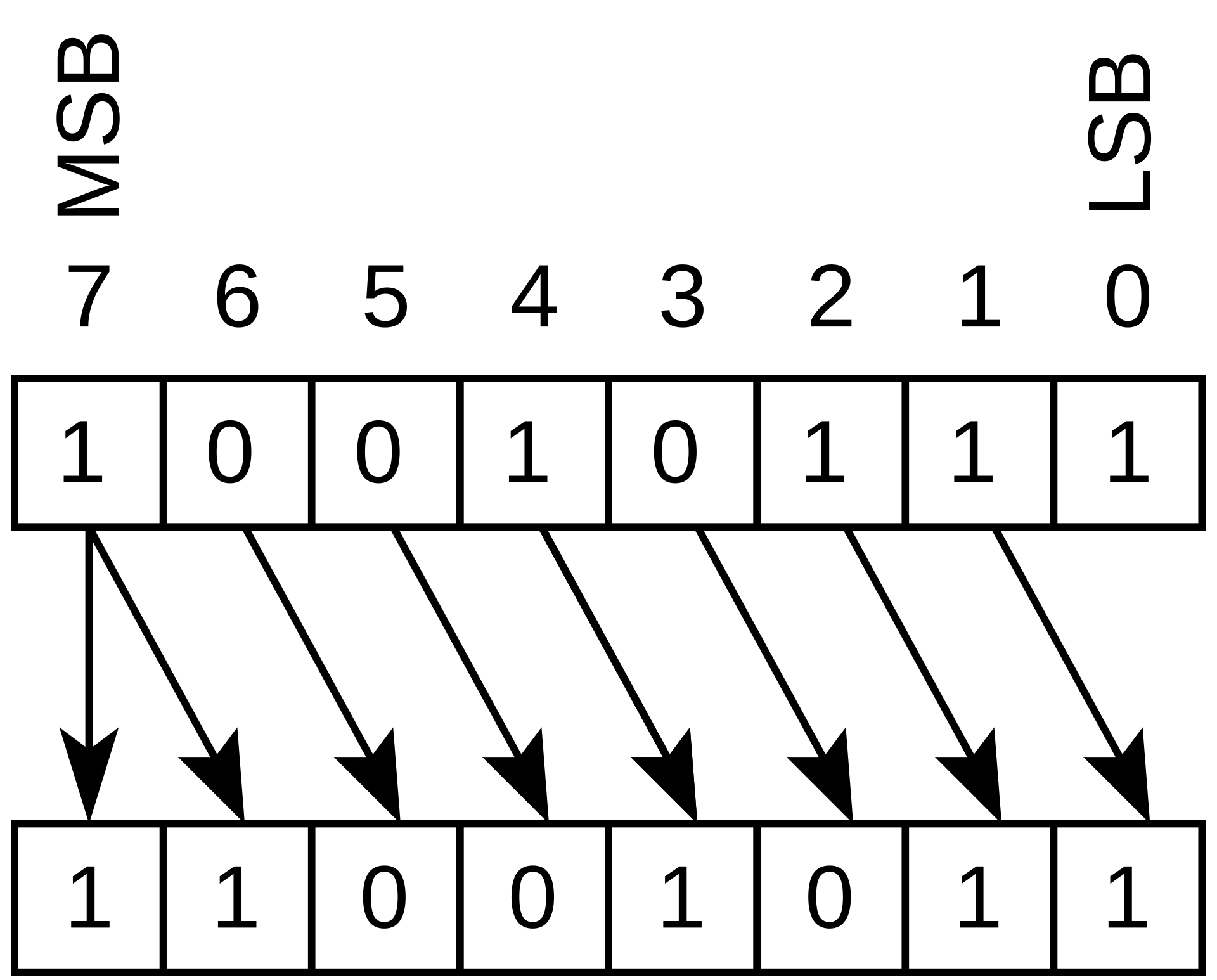
下面是算术右移，这种出现在 signed integer shift 中，对应 x86 sar

img

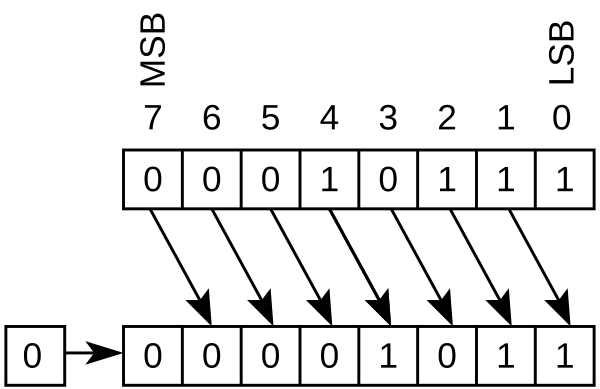
下面是对应 shr

img

浮点数的表示

https://docs.google.com/presentation/d/1fYA0ZPCARtu4DmXIwIU1IlhdnCDHeCYLmE1GKyCnV_0/edit#slide=id.g32258ac2911_0_38

img

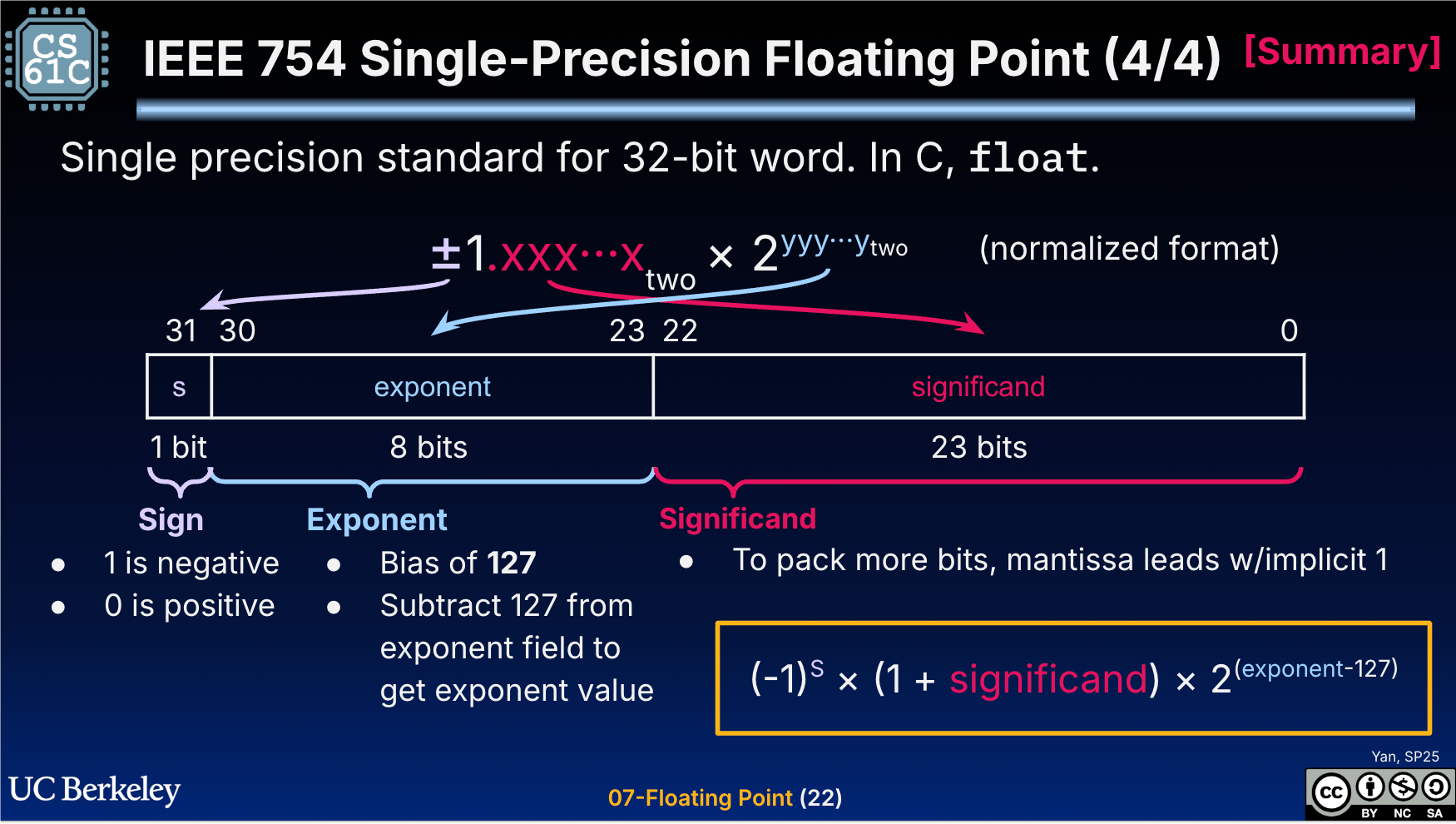
「浮点数」这个词因为被用的过多，所以我们老忘记它的定义，我们可以回到「定点数」：比如类型 Decimal(scale:100, precision: 2) 可以表示精度为 2位，所有地方 * 100 的定点数。浮点数形式则是类似上面这幅图。

对于精度 32 位的浮点数，这里定义如下

  • Sign: 表示正负号。你没想错，这里有 -0 和 +0 的区别
  • Exponent: 这种移码表示的指数部分，中文称作阶码。
    • Exponent Bias: IEEE 754标准规定该固定值为 2^(e - 1) - 1，其中的 e 为存储指数的比特的长度。
  • Significand: (2进制，1之后的数字），与前面的 1 组成浮点数的 “mantissa”（尾数）

课程有个例子，可以很好介绍这玩意：

img

关于正常的浮点数，我们其实可以有一种理解: https://jsjtxietian.github.io/2023/06/07/float/#%E4%B8%80%E7%A7%8D%E7%9B%B4%E8%A7%82%E7%9A%84%E7%90%86%E8%A7%A3%E6%96%B9%E5%BC%8F

这里可以当作 Normalized 浮点数是不同的 Buckets: [1/4, 1/2), [1/2, 1), [1, 2) ...，每个 bucket 内相当于有准确的 precision，而不同 bucket 的 precision 不同。这点也可以帮助更好理解精度和 ULP 的概念。

类型

img

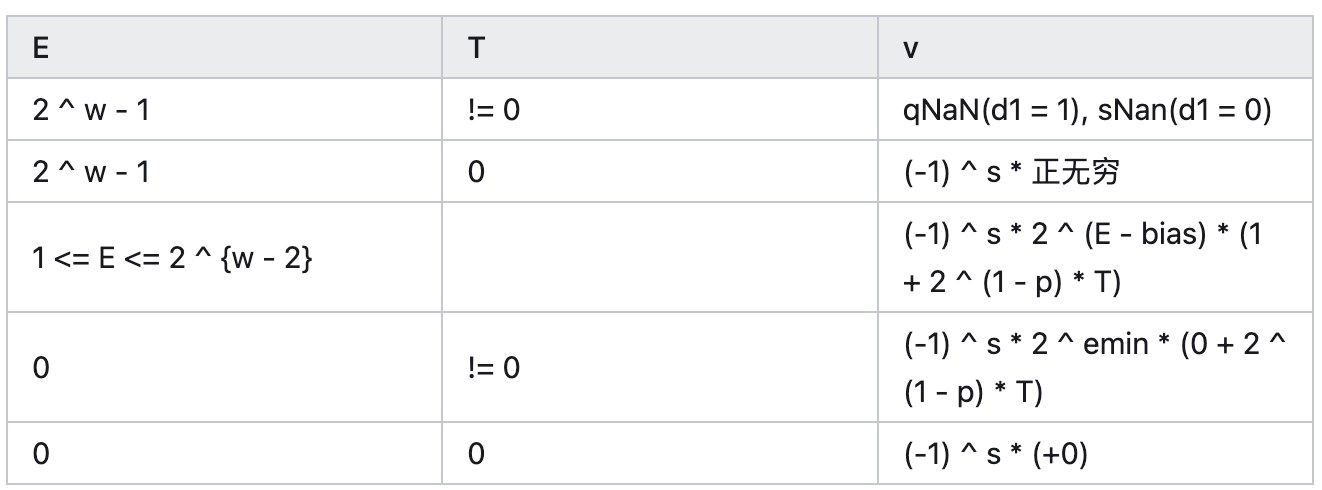
正常的数字我们已经说过了，下面介绍过大的的和过小的数字：

img

Denormalized

img

某种意义上说，这类似一种「定点数」

+0/-0

img

Inf

img

这里需要提的一点是，浮点数没有给「特别大的数字」做什么 Denormalized number:

1
2
3
4
v = std::numeric_limits<float>::max();
std::cout << v + 1.0f << '\n'; // == max
std::cout << v + v << '\n'; // inf
std::cout << std::nextafter(v, std::numeric_limits<float>::inf()) << '\n'; // == inf

NaN, qNaN, sNaN

Not-a-number

img

https://stackoverflow.com/questions/18118408/what-is-the-difference-between-quiet-nan-and-signaling-nan

用 C++ 代码看看上述的类型

frexp 会把一个数字拆分成 mantissa（包括前面的 .1 ） 和 exponent, 结束 cppreference 例子: https://en.cppreference.com/w/cpp/numeric/math/frexp

1
2
3
4
5
6
7
8
9
10
11
double f3;
double f2 = std::modf(f, &f3);
std::cout << "modf() makes " << f3 << " + " << f2 << '\n';

int i;
f2 = std::frexp(f, &i);
std::cout << "frexp() makes " << f2 << " * 2^" << i << '\n';

i = std::ilogb(f);
std::cout << "logb()/ilogb() make " << f / std::scalbn(1.0, i) << " * " << std::numeric_limits<double>::radix << "^"
          << std::ilogb(f) << '\n';

有一个比较好玩的就是 quantization 的时候，可能会有浮点数转定点数的流程，如下：

https://github.com/google/ruy/blob/2d950b3bfa7ebfbe7a97ecb44b1cc4da5ac1d6f0/ruy/test.h#L1602

IEEE 754 Total Order Float

IEEE-754 新标准定义了 Strong ordering 的比较，对应逻辑大概如下( 可以参考：https://doc.rust-lang.org/std/primitive.f64.html ）

  • negative quiet NaN
  • negative signaling NaN
  • negative infinity
  • negative numbers
  • negative subnormal numbers
  • negative zero
  • positive zero
  • positive subnormal numbers
  • positive numbers
  • positive infinity
  • positive signaling NaN
  • positive quiet NaN.

下面 C++20 也有对应的 strong_order 的实现：

https://github.com/llvm/llvm-project/blob/main/libcxx/include/__compare/strong_order.h#L56

1
2
3
4
5
6
7
8
9
10
template <class _Tp, class _Up, class _Dp = decay_t<_Tp>>
  requires is_same_v<_Dp, decay_t<_Up>> && is_floating_point_v<_Dp>
_LIBCPP_HIDE_FROM_ABI static constexpr strong_ordering __go(_Tp&& __t, _Up&& __u, __priority_tag<1>) noexcept {
  if constexpr (numeric_limits<_Dp>::is_iec559 && sizeof(_Dp) == sizeof(int32_t)) {
    int32_t __rx = std::bit_cast<int32_t>(__t);
    int32_t __ry = std::bit_cast<int32_t>(__u);
    __rx         = (__rx < 0) ? (numeric_limits<int32_t>::min() - __rx - 1) : __rx;
    __ry         = (__ry < 0) ? (numeric_limits<int32_t>::min() - __ry - 1) : __ry;
    return (__rx <=> __ry);
  }

Ulp

其实这里可以看看这篇文章（这篇文章没有介绍什么是 ULP，但是对理解这块帮助不小）： IEEE754标准: 三, 为什么说32位浮点数的精度是”7位有效数” - 等夏天再见啦的文章 - 知https://zhuanlan.zhihu.com/p/343040291

img

这里代码也可以处理成 std::nextafter，我们可以看看 Arrow 的 ULP 例子( FLT_EPSILON 也是和这个有关的）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
template <typename Float>
bool WithinUlpOneWay(Float left, Float right, int n_ulps) {
  // The delta between 1.0 and the FP value immediately before it.
  // We're using this value because `frexp` returns a mantissa between 0.5 and 1.0.
  static const Float kOneUlp = Float(1.0) - std::nextafter(Float(1.0), Float(0.0));

  DCHECK_GE(n_ulps, 1);

  if (left == 0) {
    return left == right;
  }
  if (left < 0) {
    left = -left;
    right = -right;
  }

  int left_exp;
  Float left_mant = std::frexp(left, &left_exp);
  Float delta = static_cast<Float>(n_ulps) * kOneUlp;
  Float lower_bound = std::ldexp(left_mant - delta, left_exp);
  Float upper_bound = std::ldexp(left_mant + delta, left_exp);
  return right >= lower_bound && right <= upper_bound;
}

我们可以想象一个判断的例子 googletest，这里浮点数要求精度在 4ULP 内：https://github.com/google/googletest/blob/main/docs/reference/assertions.md

Rounding 和计算误差

Rounding 又叫「舍入」，如下图

img

GNU 严格规定了加减乘除等单次浮点运算引入误差必须小于等于0.5 ULP，单次函数计算的引入误差最大不超过2 ULP。实际上 FMA 操作的好处也是「避免两次 Rounding」，很神奇吧。

杂项: 除以零

姜特德有一篇最烂的短篇叫做除以零，这篇 SF 导致我无法停止对他水平的抹黑，到现在还认为他是低配的 Greg Egan。

对于 Python 来说，除以零会出现下面的错误：

1
2
3
4
5
ZeroDivisionError: float division by zero
>>> 1.0 / 0.0
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ZeroDivisionError: float division by zero

然而，在 C++ 中，对应的操作是 inf

1
2
std::cout << 1.0f / 0.0f << '\n'; // inf
std::cout << 1.0f / -0.0f << '\n'; // -inf

这里整数进行 / 0 可能会有 SIGFPE:

1
2
std::cout << 1L / 0 << '\n';
std::cout << 1U / 0 << '\n';

Reference

  1. Standard: https://www-users.cse.umn.edu/~vinals/tspot_files/phys4041/2020/IEEE%20Standard%20754-2019.pdf
    1. 网上有人翻译的二手文章：IEEE 754 - 2019 浮点算数标准 - nicholaswilde的文章 - 知乎https://zhuanlan.zhihu.com/p/480834719
  2. Cs61c slide: https://docs.google.com/presentation/d/1fYA0ZPCARtu4DmXIwIU1IlhdnCDHeCYLmE1GKyCnV_0/edit#slide=id.g33006864fd4_0_469
  3. IEEE754标准: 三, 为什么说32位浮点数的精度是”7位有效数” - 等夏天再见啦的文章 - 知https://zhuanlan.zhihu.com/p/343040291 —> 一篇二手文章，但感觉对理解浮点数很有帮助