Sorting in Database System: Part2 External Sort
前文链接: https://blog.mwish.me/2024/09/27/Sorting-in-Database-System-Part1/
对于 Internal Sort 来说,如果排序的数据量过大,那么就需要走 External Sort。其实大部分教科书上都介绍过 External Merge Sort,所以它基本工作方式和怎么和 Loser Tree 结合都很好想象了。对于 External Sorting,我们可能还要考虑:
- 比如经典的教材中,io 优化(写入 - 读取的时候做相关的优化)
- 现代设备的影响,导致存储设备有着充足的吞吐带宽,在预读之类能有用的情况下,保持 CPU fast 也很有必要了
这里也讨论了:
- 如何生成 Run ( Run Generation)
- 在要处理的输入大于内存但多的也不是很多的时候,如何优雅的从内存降级到部分写入盘上
比较新的论文是 CWI 发表在 icde 上的文章 「These Rows Are Made for Sorting and That’s Just What We’ll Do」。不过本文也是接在上一篇文章 Part1 上的。
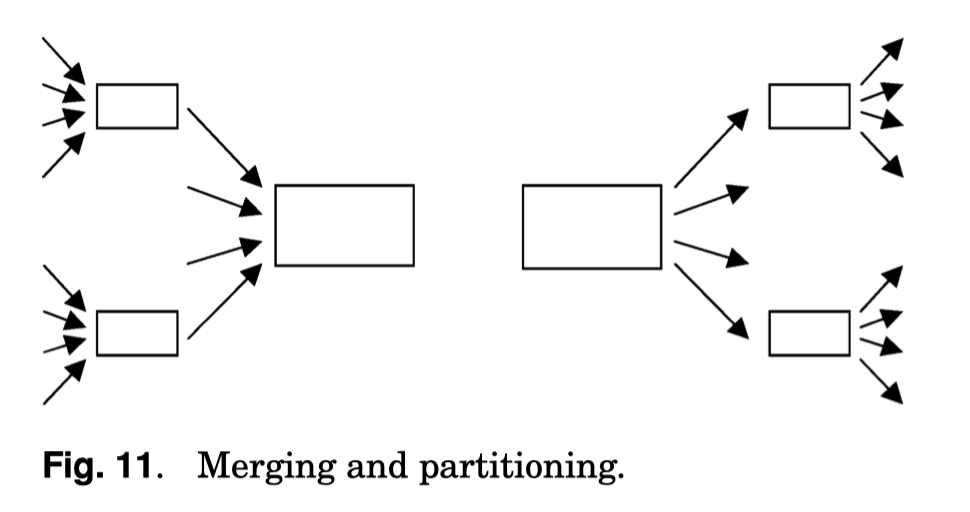
Partitioning Versus Merging
基于 Partition 的 merge sort 其实类似于 Hash Agg 的那种方式,不同的是,这里分片的方式是根据 order-preserving 的 distribute function 来做,然后最后在内存的部分也需要被 Sort (像 Datafusion 和 Velox 的 Hash Aggregation 实现)。在这种情况下,本质上给 Hash 用的策略也能用到 Sort 上,比如 Spark 可能会从 Hash Join 降级到 Merge Join,很多 hash 的优化,比如 Spill 或者拆分 bucket 的策略也可以用在 Partition based sorting 上
下图是一个 Merging and Partition 的比较。这里核心其实在用一种 Range-Based Shuffle 的方式切分内存的数据到排序的 Partition 上。这里也说到,之前 Hybrid Hash 的一些降级优化、Histogram 优化可以用到 Partition 策略上。可以参考上一篇 https://blog.mwish.me/2024/12/25/Hash-joins-and-hash-teams-in-Microsoft-SQL-Server/ 。不过 Bail-out 这里策略似乎不太会出现,因为排序本身能够处理这种 skew 的场景了( If a partition cannot be split further, this partition must contain only one key, and all records can be produced immediately as sorted output. )
作者说,本质上 Merge Join 如果用 Partition,也能采取 Hash Join 的很多策略:
- Spill 之类的策略
- Team
- Bloom Filter (但我觉得对于 Range 来说应该是 Histogram?)
但很少有人这么做,因为之前没有人这么做过( Nonetheless, partition-based sorting hasn’t been extensively explored for external sorts in database systems, partially because this adaptation hasn’t been used before. However, in light of all the techniques that have been developed for hash operations, it might well be worth a new, thorough analysis and experimental evaluation ),这块的研究就一直没啥人搞。我个人感觉现在一些 Range-Based Shuffle 之类的可能和这套东西思路比较相似。
Run Generation
首要的任务是从数据输入的 Operator 生成 Sort-of-runs。我们有快速排序、归并排序、堆排序三种基于对比的排序算法。快速排序本身是就地的,而归并排序在 Merge 阶段有的实现可能需要额外空间(也可以不要)。平均而言,对内存大小为 M 的 Sort Buffer,它们能生成大小大概为 M 大小的 Sorted Run。
Replacement Selection
有一种方式是 Replacement Selection,在教科书上也找得到这种方式的实现。见:
- https://opendsa-server.cs.vt.edu/ODSA/Books/Everything/html/ExternalSort.html
- https://www.cs.bilkent.edu.tr/~canf/CS351Fall2010/cs351lecturenotes/week4/index.html
需要阅读下去,我们需要援引上面的材料 (1) 介绍一下 Replacement Selection
- 假设系统中有 Input Buffer,用于 Sort 的 Memory Buffer,Output Buffer
- 在 Memory Buffer 构建一个最小堆
- 输出最小的元素到 Output Buffer,然后查看 Input Buffer 的下一个元素
- 如果下一个元素大于刚输出的元素,那么可以加入堆
- 否则,需要输出堆中所有元素,然后准备生成下一组 Run
按照 snowplow argument 证明,这个算法能输出平均长度为 2M 的选择元素。这里还讨论了一个性质,在这个算法开始的时候,可能生成的 Run 会比较小,后续就会慢慢变大。
上面是 Replacement Selection 的正常算法,本文虽然没有介绍,但描述了一些别的性质和优化:
- QuickSort 和 MergeSort 本身内存管理相对简单,Run Generation 的时候,相当于构造 sorted run page 的时候,先去 build indexes (ties?),然后排序这些 indexes,最后 build run,仅需一次内存拷贝。这比较直接,感觉写一遍本身都没啥开销
- Replacement Selection 输出的记录本身可能含空洞,所以需要对记录本身做管理,如下图,可能某些情况空洞会很多。这里内存结构可能是一个 Loser-Tree 作为 Priority Queue,使用 Normalized Key 或者 Poolmans key 之类的技术。这里没有画 Free space management,然后用 Indirection vector 来做一层映射,在右图的空间做空闲空间管理。这里还需要 free space management 来管理内存中的这些记录,因为 replacement selection 会延迟输出这些记录
- [Larson and Graefe 1998] 提到了空间利用率占到 90% 的一些方式
- 另外,如果这块比较难处理,可以先构成一些 Mini Run,比如在 replacement selection 之前先对 input page 做局部排序 [Larson 2003]. 这里也提到本身可以通过 load-sort-write 或者 replacement selection 构成 一些 cache-sized runs,然后通过 poor mans normalized key 提供 CPU Cache 访问的优化。
- 这里还提到 batch 输入来减少 cache miss,但也提到,在 priority queue 的结构上,batch 不一定是个特别好的 idea,因为这里排序本质上还是个基于行的操作。
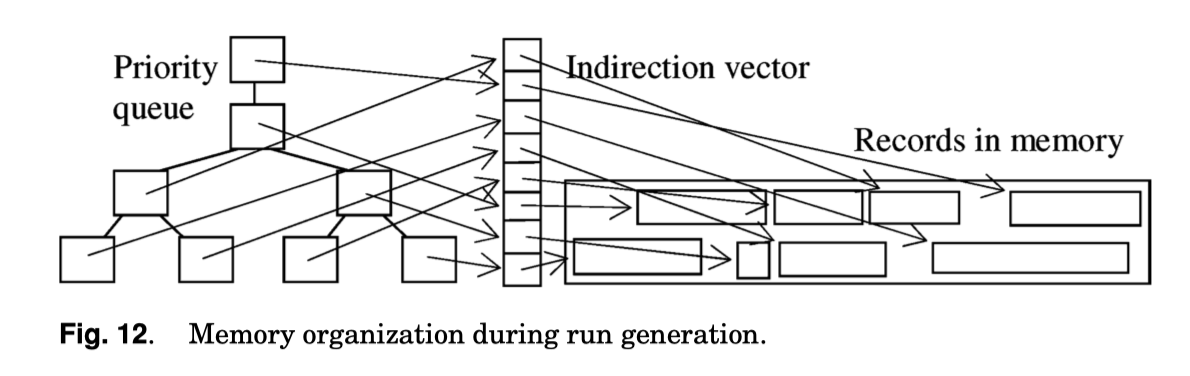
本质上,和内存排序类似,这里相当于对长度 = 1 的 sorted runs 构建新的 run,如果有一些局部有序的输入,可以把他们当成更长的 Sorted run,这里类似前面在上一节介绍的。
然后这里还提到了 Replacement Selection 的一个比较好的性质,因为 Run Generation 是连续的输出,而不需要 read-sort-write 循环,这里可以引入一下性质:
- permits concurrently running the input query plan and the disks for temporary run files
- Has desirable effects on both parallel query plans and parallel sorting
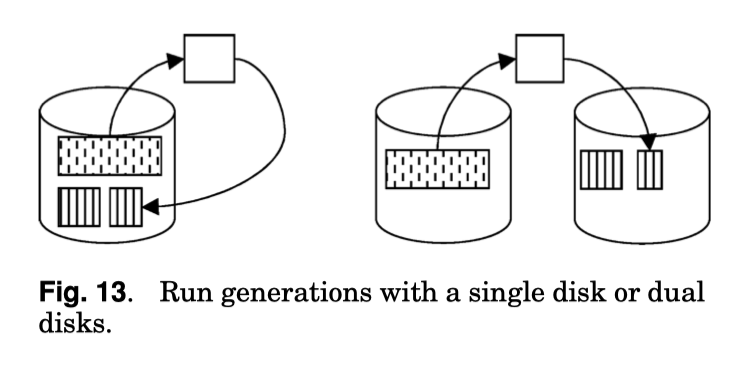
这里我还有些困惑,直到看了下图,大概是这样比较好分离读写,而单个 Merge 的 read-sort-write 总有盘是 idle 的(但 merge 之类的也可以并行啊,其实没完全懂)。
Graceful Degradation
这里需要最小化内存不够,但又不是那么不够的的时候的开销。
这里讲到了优化器侧非常有意思的一段话,我看了两遍才看懂
- 如果排序操作的成本函数存在显著的不连续性(例如,当输入数据略大于内存时,成本突然增加),内存管理策略中需要设计大量的特殊代码来避免这些高成本的排序操作。
- 在查询优化阶段,基数估计(cardinality estimation)的误差会加剧这个问题,因为优化器可能无法准确预测排序操作的成本。
- 如果排序操作的成本函数是平滑的(即 CPU 和 I/O 负载随着输入数据的增加而连续增长),实现有效的内存分配策略会变得更加简单。
- 处理特殊情况(如输入数据略大于内存时的高成本排序)不仅需要额外的开发时间,还需要大量的测试工作。数据库用户可能会观察到某些查询或排序操作异常昂贵,这需要开发人员提供解释和解决方案。
上面这段话也阐述了 Graceful Degradation 对于整个数据库系统的重要性。
- 最后两个运行的特殊处理:
- 最后一个 Run 保留在内存中,不会写入磁盘。
- 倒数第二个 Run 在为第一次合并步骤腾出足够内存时被截断。
- 交错读写:
- 如果使用 read-sort-write 循环,读写阶段实际上是一个交错的过程。写入 Run File 的操作可以在读取输入结束时立即停止。
这里我其实觉得 Truncate 是个好路子,但是「倒数第二个」这个说法我一直想不清楚为啥,我觉得可以理解为申请内存的时候可以 spill 一部分(不是正在 build 的?) sorted run 到盘上。
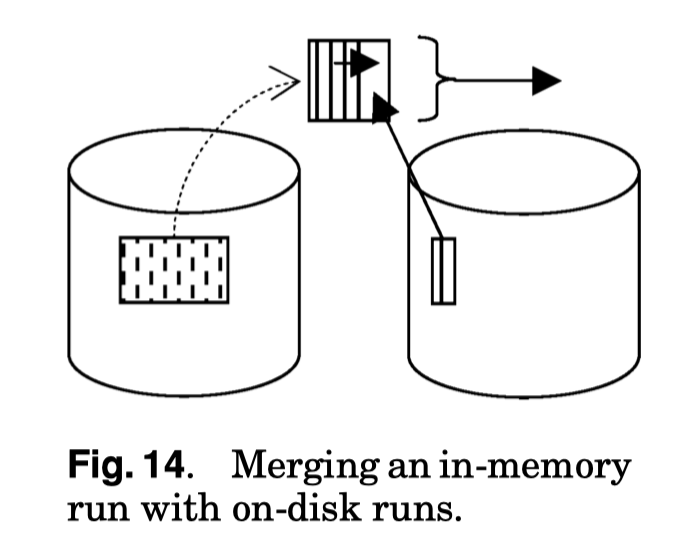
Merge Patterns and Merge Optimizations
论文发表在 06年,这节开头就是句很有意思的话:
It is widely believed that given today’s memory sizes, all external sort operations use only a single merge step.
天啊,难道不是吗!!! (我最近还真遇到了 MergeReader 内存占用高的问题)
If a sort operation is used to create an index, the belief might be justified, except for very large tables in a data warehouse. However, if the sort operation is part of a complex query plan that pipes data among multiple sort or hash operations, all of them competing for memory, and in particular, if nested queries employ sorting, for example, for grouping or duplicate removal, multilevel merging is not uncommon.
大概意思是那种 spill 多的 multi level merging 内存管理也是比较复杂的。论文吧这里输入拆成了几个部分:
- Input phase with run generation
- Merge phase with all intermediate merge steps
- Output phase with the final merge step
下面也有不同 sort key 的 Sort + Merge Join 流程(有的地方会把部分排序输入抽象成一个算子 Partial Sort,这个感觉与论文不完全有关,知道就行)。
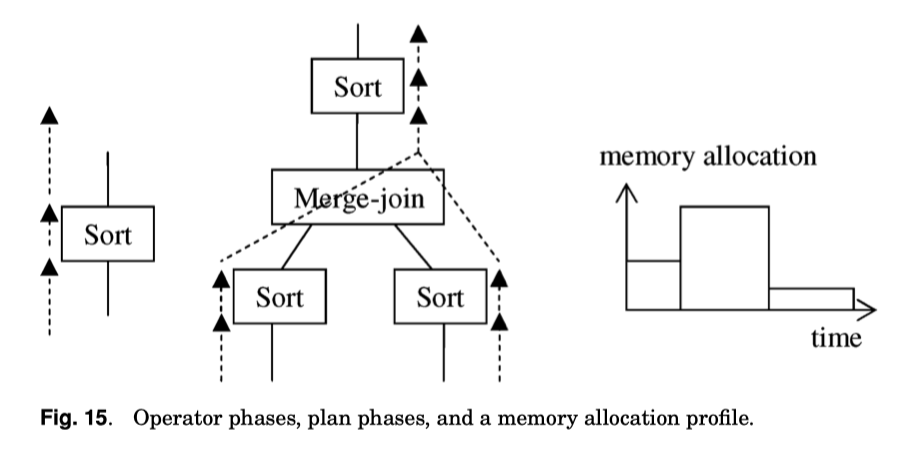
这里也预测了对应的内存分配模式:
每个排序操作的内存分配模式可能类似于图 15 右侧所示的模式:
- Input phase
- 适中的内存分配(取决于输入数据的来源)。
- Merge phase
- 完全的内存分配(使用所有可用内存)。
- Output phase
- 相对较小的内存分配
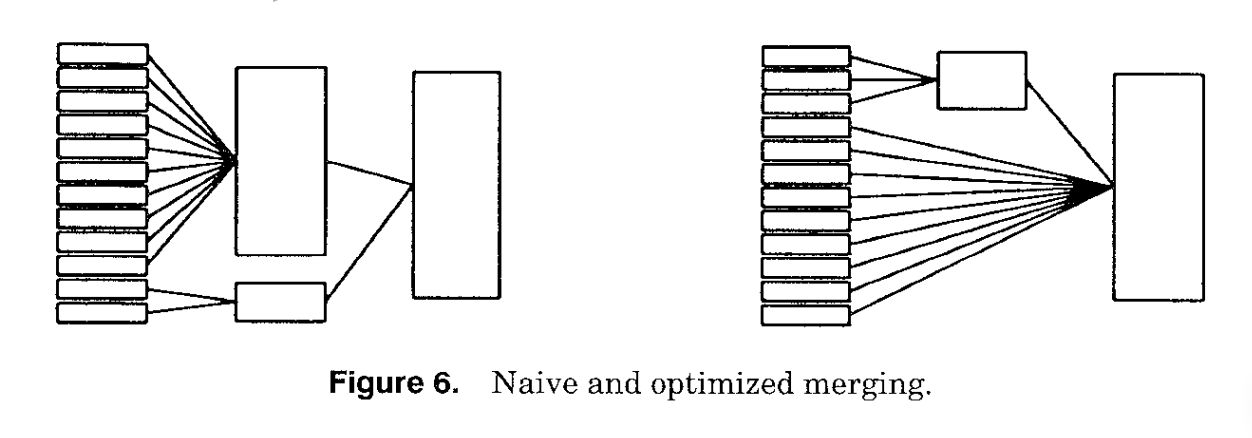
论文这里还提到了 semieager merging 和 eager merging,我看都看不懂,翻了一下:https://courses.cs.washington.edu/courses/cse544/04sp/papers/graefe93.pdf / https://cs.uwaterloo.ca/~david/cs848s13/graefe.pdf . 这里是针对 multi-level merging 的优化。
Merge 最终还是希望整个 operator 只有一个 Sorted Run 输出。这里本质上也有 trade-off,如果有所有的输入
- 启发式的方法是总是合并最小的 existing runs
- 使用最大的 fan-in
否则可以:
- 一种替代策略是合并大小最相似的 Run,而不考虑它们的绝对大小。这种策略试图减少最终的比较次数
这里还提到了 sorted run sort-key range 和 virtual sub range 的概念:
- 比如对于 Sorted Run,merge 的时候不应该去 merge min-max 无 overlap 的,它们原则逻辑上甚至可以被视作是同一个 sorted run
- 这种合并的 Run 可以被称为 “virtual” run,拼凑它们的操作被称为 virtual concatenation。这里需要记录 Run 的 Low-sorted key 和 High-sorted key. 这里也可以用纯 Poor man’s key 的形式记录
- 这种方式对 random inputs 来说没有太多的优化,但是对有一些顺序的输入来说有一定的优化
- 这里对于 sorted run,按照值域也可以切分出内部的 sub-range,通过这个 range,来增加调度的单元,减少合并的粒度
- G.G. 还举了个脑洞,把这个内部的 merging 和 range partition 结合起来。下面有个例子,这个例子中,稀疏的流可以去合并到稠密的流里( recall 上一节的,有序的流大小不同,所以合并的策略可以不同)。
consider an external merge-sort with memory for a fan-in of 10, and 18 runs remaining to be merged with 1,000 records each.

I/O Optimizations
这节聊的有点 hack,介绍了一下 io-size、预读和效率的关系,通过这个选出最好的预读 size。然后介绍了怎么用 btree 的代码来规划 Run File 的 io-prefetch。看得比较晕。