Compiler Optimizations: Power, Limits, Auto-vectorize

本文是系列文章的第三篇，前两篇文章：

本篇其实还没到 Part 1，估计算是 0.8 了。本篇文章会介绍编译器能够做的一些优化和优化的限制，然后介绍 LLVM 的 Auto-vectorize。下一期会开始介绍 AVX2。

在 part-0.5 中，我们介绍了使用手写 Fast-Scalar 代码的例子和代码。实际上，在 llvm 需要复现类似的测试结果，需要关掉 LLVM Auto-vectorize，因为后者可能会帮助生成一些相似的代码。这就是编译器的魅力。但是你会发现，开不开对于浮点数都是没有区别的，我们之后会介绍，浮点数的计算因为受到精度之类的东西的影响，在没有 -ffast-math 的情况下，很多优化浮点数是不让做的。（说个和本题无关的，昨天看 patch 的时候竟然发现 C++20 之前 unsigned 整数转 signed 是实现定义的…而且实现定义和 ub 还不是一回事，这个震撼我心了）

这篇的主要材料来源于 Matt Godbolt 的博客和 Ethz / CMU 的课件. 本文本来11月就该写完了，因为我加班加的有点烦，中间摆烂了很长一阵子，这两天回家缓了缓才觉得应该干活了。拖了很久实在不好意思…

编译器的优化和限制

编译器能够进行很多有效的优化，但是其中也有很多限制。「意识」到编译器能够进行的优化有助于我们写出快速的代码，同时，也让我们不至于因为性能搞得代码看上去特别搓。

简单的说，我个人总结就是：

  • 编译器会尝试替换昂贵的操作
  • 编译器知道的比较多就能更好作出优化（参考 LTO、PGO）

具体可见： https://dl.acm.org/doi/10.1145/3371595.3372264

有个比较好玩的，作者写的关于 LTO 的话：

Despite being a relatively established technology (I used LTCG in the early 2000s on the original Xbox), I’ve been surprised how few projects use LTO. In part this may be because programmers unintentionally rely on undefined behavior that becomes apparent only when the compiler gets more visibility: I know I’ve been guilty of this.

只能说 Godbolt 中肯。function call 通常是阻碍优化的部分，这个可能包括的部分有很多，你得知道函数是不是 pure 的，参数是否是 const 的，会不会修改你的参数。里面是否有原子操作之类的东西，会有那种禁止你 ordering 的东西。inline 之类的。这方面有 LTO 的话会方便很多（毕竟你自己优化能优化到哪去呢？）

这里还是建议直接看原帖，原帖重要部分是给了几个优化的实际例子，我还是比较建议通读完的，这里还有个重点是浮点数：

This does rely on the fact that separating the totals into individual subtotals and then summing at the end is equivalent to adding them in the order the program specified. For integers, this is trivially true; but for floating-point data types this is not the case. Floating point operations are not associative: (a+b)+c is not the same as a+(b+c), as—among other things—the precision of the result of an addition depends on the relative magnitude of the two inputs.

浮点数的操作都和很多东西相关，不开 -ffast-math 之类的其实不好优化的。因为编译器还是在不修改程序的语义下进行优化的。

文章中还有几个比较重要的部分：

当然，乱优化浮点数可能会产生非预期的结果，比如 NaN 的处理可能会产生一些非预期的行为。

此外，影响优化的一点包括 memory alias:

img

这种不确定 alias 的情况下，可能不是特别好优化，可能编译器会加上一些 flag 或者 Runtime Flag，但我理解有来自用户的先验知识，能够帮助编译器没有负担的产生更快的代码。

img

当然，你有一些宏可以用上，这里可能也可以帮助你来展开循环，比如 #pragma ivdep

img

LLVM Auto-Vectorization

15-721 的课件有一张比较有意思的图，但这张图实际上是错误的，编译器在这方面其实还是蛮聪明的：

img

LLVM 有一种 Runtime checks of pointers 的能力，它会编码一个 Runtime 的 checking，如下。

https://llvm.org/docs/Vectorizers.html#runtime-checks-of-pointers

我希望我们能回忆起来上一节的优化内容，上一节里面我们展示了一个手动的对非向量化代码的优化：https://blog.mwish.me/2023/11/15/Fast-Scalar-Code-and-Compiler/#Parquet-BYTE-STREAM-SPLIT-%E5%8A%A0%E9%80%9F

我们可以看到上述优化的代码的一些思路：

  1. 拆分计算，把 vectorize 的计算拆分成为一组计算 Load 一大组 —> 对这组数据进行计算 —> Store 内存
  2. 如果是 SIMD 或者利用指令级并行，那么计算出某个核心的计算逻辑对应的 port 数，然后去并行执行它们
  3. 上述操作如果是在 TP 点查操作中其实不一定划得来，因为没几个操作跟你并行，即使是 TableScan -> Filter 这种也是。但是可能 AP 这种 workload 本身就有一大批数据需要计算的，所以可以拆分成这样每个 batch 批量执行的计算。这个批量大小和 CPU、Port、访存操作有关。如果输入数 % batchSize 还有剩余的话，可能会需要接一个 non-vectorize 的 epilogue

比较有趣的事，LLVM 自动向量化会尝试产生一个类似下列的结构：

  • Vectorize Body
  • Vector Epilogue
  • Scalar Epilogue

img

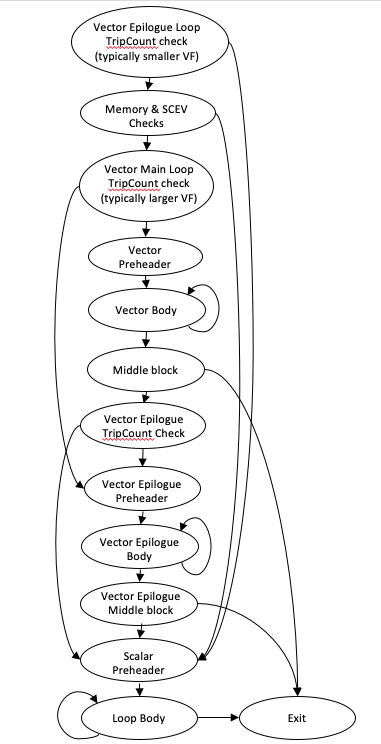
LLVM 会按照上述内容来优化。知道这个之后，我们去看看 LLVM 官方的 Vectorize 文档：https://llvm.org/docs/Vectorizers.html#features

下列的代码是可以 vectorize 的

  • Loops with unknown trip count
1
2
3
4
void bar(float *A, float* B, float K, int start, int end) {  
    for (int i = start; i < end; ++i)    
        A[i] *= B[i] + K;
}
  • Reductions
1
2
3
4
5
6
int foo(int *A, int n) {
  unsigned sum = 0;
  for (int i = 0; i < n; ++i)
    sum += A[i] + 5;
  return sum;
}

这里如果是 Reductions ，那么 add, xor 之类的操作，它会抽出一个 vectorize 组（类似 unsigned[dop] sum )，然后在上面操作的时候，避免操作同一个值。注意这里对浮点数是不能这样操作的（除非开了 -ffast-math）

  • Inductions
1
2
3
4
void bar(float *A, int n) {
  for (int i = 0; i < n; ++i)
    A[i] = i;
}

这种能向量化（好像很合理）

  • If Conversion
1
2
3
4
5
6
7
int foo(int *A, int *B, int n) {
  unsigned sum = 0;
  for (int i = 0; i < n; ++i)
    if (A[i] > B[i])
      sum += A[i] + 5;
  return sum;
}

control flow in the innermost loop 这里可以 vectorize，这里可以参考博客：https://sbaziotis.com/performance/a-beginners-guide-to-vectorization-by-hand-part-3.html

  • Pointer Induction Variables
1
2
3
int baz(int *A, int n) {
  return std::accumulate(A, A + n, 0);
}

对指针和标准库能很好处理

  • Reverse Iterators
1
2
3
4
void foo(int *A, int n) {
  for (int i = n; i > 0; --i)
    A[i] +=1;
}

对反向操作很好处理(跟 rsy 聊的时候他还告诉我 reverse 方向的 prefetch 可能不如正向的 prefetch，学到很多）

  • Scatter / Gatter
1
2
3
4
void foo(int * A, int * B, int n) {
  for (intptr_t i = 0; i < n; ++i)
    A[i] += B[i * 4];
}

-mllvm -force-vector-width=# 的情况下这里可以控制开启，否则它可能不会开，因为它可能发现 cost 划不来（gather scatter 可能会比较昂贵）

多种类型的混合会根据代价来估计

  • Partial unrolling during vectorization
1
2
3
4
5
6
int foo(int *A, int n) {
  unsigned sum = 0;
  for (int i = 0; i < n; ++i)
    sum += A[i];
  return sum;
}

这个长得和前面 Reduction 很像，但这里是说，会按照 port 的数量，来拆分并行度。

这些只是我选了想记住的一部分，需要知道具体细节可以浏览原来的文档。

References