VLDB'23: Query Partition in Napa
Google 在 VLDB’21 年发表了 Napa 的论文: Napa: Powering Scalable Data Warehousing with Robust Query Performance at Google。Napa 本身定位是一个对 MV 支持很好的数仓,它用 LSM 来存储对应的内容,读查询通常是 Scan 和 Multi-key Lookup(下面是 Multi-key Lookup 的一个例子,感觉是很 ads 的需求)。
在查询延时上,Napa 的需求比较高,通常它需要在压秒级的时间内完成一些查询。在数据上,Napa 有数百个 databases,其中有数千个 Table 和 MV.有些表大小甚至到达了几 PB。这些表也会被上游流系统很频繁的更新。用户希望数据有一定的实时性。为了满足这个需求,Napa 实现了 LSM-Tree 和基于 LSM 的 MV 维护引擎。

上述 Figure1 例子中,Napa 以 K1, K2, K3 为主键,并按照 K.. 排序。这里主要需求是对这一组查询(K1, K2 的前缀 key)采取并行查询,通过打大并发降低对应的延迟。
这里有一些比较重要的部分:
- Query-specific partition: 根据查询生成对应的并发度和 Partition,来 match 对应的 SLO
- Evenness: Partition 需要能够处理 skew 的情况,e.g. Figure1 中
<K1 = 1, K2 = 20>数据可能有几百 GB - Progressiveness: 这个有点类似 Planner(但我其实不太懂,我理解是有点像,但也可能根本不一样)。算出一个 Perfect 的 Partition 是很费时间的,只要算出来预估差不多满足 SLO 需求就可以停手去执行了。所以这个算法是渐进式的。
在本论文之前也有很多 database partition 的需求,包括 write-time partition(主动 partition, compaction, snowflake 风格的 micro-partition) 和查询并行. 作者认为这里解决的问题不完全一样(但我觉得肯定可以整合到一起),假如用 Partition 的方式解决并行问题的话:
- Partition Unit 小的话, Metadata 维护开销很大,访问 metadata 的 latency 会增加
- Partition Unit 大的话,如果按照 Partition 来并行的话,可能读数据的 latency 下不去
论文中实验也表明,用太细的东西做 plan 的话,这部分 planning 开销也会升高。这部分 Napa 和 Btree 结合起来了,它的 LSM Sorted Run 本身是个 DataBlocks + Btree (看着像是用 Btree 组织了一组 SST,类似 Kudu 的 Block 存储,会根据 Btree 来组织,见 https://github.com/apache/kudu/blob/master/docs/design-docs/tablet.md#handling-mutations-against-on-disk-files 。RocksDB 的 Index 也大概是这种方式组织的),每层有一些统计信息,越上面越粗略。Napa 通过这种方式来做切分。如果 Btree 上层节点足够了就用上层的,上层切不出来或者不够详细就要访问 Btree 下层。(之前在 bg 好像搞过类似的,不过它这里好处还是 immutable + 和统计结合)
相关工作
并行处理的主要工作基本上是并行化 SQL + SIMD 模型来查询。早期的批处理工作类似 Map Reduce 一个 idea 就是切分输入并并行。
在数据库迁移到云上或者做大规模处理的时候,流行的方式是对 Key 做 {Hash/Range} Partition。这种方式也允许用户做 Collocate Join,并且能够尽量避免 distributed transaction ( For OLTP workloads, graph-based [6, 20] and skew-aware [19] partitioning approaches have been developed to minimize the number of distributed transactions. )。这种方式倾向于写时维护 Partition(废话,TP 分布式事务或者多走了一轮开销大是这样的)
在查询的时候做 Partition 没有那么直接的工作,比较接近的工作是 database cracking。本作准备用 RL 糊屎来解决不同用户的输入。
Napa
Napa 吹了一下自己系统几个需求:
- Robust Query Performance: 亚秒级响应,adhoc 查询
- System Flexibility: Napa 的性能三角,允许拿钱之类的换 freshness
- High-throughput Data Ingestion: Napa 会有很大的写入量
Napa 的每个 Delta Set 相当于 LSM 的 Sorted Run,它们会被组织成 btree。每个 Delta 的 Btree 内部是没有 MVCC 的(不像 RocksDB 可能会把同一份数据 Duplicate 不同时间戳的多次操作)。为了支持 Statistics 的需求,这里会设计每层的 Statistics,父亲级别 Agg 子层级的统计信息。
建模
LSM
在 napa 中,每个文件是 immutable 的,在 napa 的设计中叫做 Delta。对应格式是一个 btree,对应 napa 中的一个时间范围,和文件的 indexes。Napa 采用了 Tiered Compaction 的形式(话说之前看 G.Goetz 的简历上说他现在还在维护 napa 的 compaction),它时间戳和 Compaction 逻辑维护形式有点类似于 ClickHouse,文件落到 Napa 的时候拿到一个统一的时间戳([T1, T1]),Compaction 的时候产生新的时间戳 Range([T1, T3])。
当 Table 存在 unique key 或者 primary key 的时候,这里需要做读的时候 dedup (类似 Hudi MOR)。Napa 似乎不会对系统做假定(类似 Hudi 不假定前面是 MOR 还是 COW?)。
作者认为 LSM 增加了 Query Partition 的复杂度。主要还是因为它不是 btr 那样单层的模型,一个 key 可能存在多处。这也给查询 evenness 的估计带来了一定的复杂度。最后一点是,不同层的 Sorted Run 可能因为数据分布不同,在它们上面 Plan Partition 的难度也不同。
查询

Napa 有一些单机的 scan worker :
- 能够执行:Selection, projection, partial (local) agg
- 输出可以是别的 downstream,可能会被 full agg, sort, join 之类的消费对应的计算
Napa 的查询优化器会尽量按照 PK 把用户的 Predicates 做成前缀(感觉有 pk 的表大家都这么搞的,但是这里有点类似 PG,<pk1, pk2...> 里面,即使只有 pk2 == ..., 它也会尝试构建 Prefix),在上述查询中有下列的 transform。

在做 Partition 的时候,因为 filter selectivity 的不同,scan worker 配置的资源不一样,所以查询的时候 partition 的情况也不同(这里大概可以理解成,论文里的 size 是原始数据的大小,应该不是 filter 之后的大小)。所以最佳的 partition unit size 可能从 10MB - 1GB。此外还有个问题是查询的 skew。Napa 对于 <c, d> 这种表,当 d = d3 的时候,构建的前缀可能覆盖了整张表的大部分空间(那你就别这么搞啊…)这也表明,Partition 规划需要是渐进式的,能够防止构建的粒度过细。
Napa 认为 write-time partition 并不好处理这种 case,主要原因还是它:
- 写的时候切的太细的话或者太粗的话,读者需求都不一定完全满足。毕竟都是 adhoc query 和不同的资源在到处飘
- Hash Cluster 之类的情况不太能处理 skew 或者
d = d3这种查询。可能导致 Partition 规划的开销高,算起来还因为 Partition skew 性能不太好。
然后 G+ 的人不装了,扯了这么久才介绍自己的需求:
Note by this example, we have established that partitioning is highly specific to query under consideration and existing writetime partitioning is inadequate for workloads with a wide spectrum of query workloads
总之 G+ 的人是想要在 PROGRESSIVE PARTITIONING 中发掘 Partition 的需求,渐渐发现「Plan Partition 快、查询也满足 SLO」的真相
Progressive Parititoning
那么,Napa 已经有:
- 每个 Delta 有一个 B-tree, 维护指向每个 PAX layout Block 的 size 等 Statistics
- 一定数量的 scan workers, 和从 workers + QoS 可以推断的目标 Partition 数量 P
- margin ratio: theta, 用于控制衡量 Partition 的结果,表明预估的大小和实际分片大小可能的偏差。算法的预期是随着运行让这个误差尽量小。满足预期的时候,算法推出
算法的预期是:
- 给定查询 Q,算法能够切分 D 组 Deltas 成为 P 个 key-range Partition, error margin 对应是 theta
- 预期大小 == 根据 Btree Indices 的大小和 combine-key 来推断
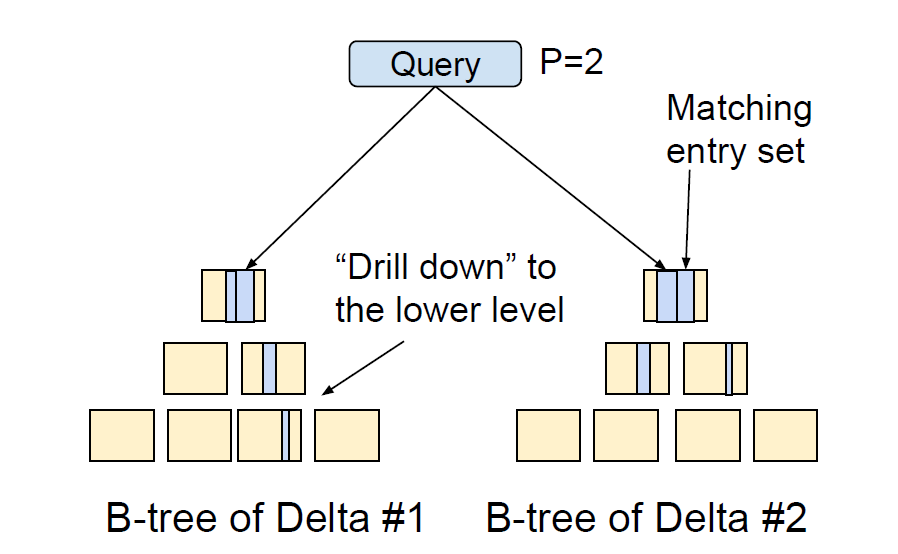
Figure 4-5 演示了算法工作的流程。Figure 4 展示了有四个 Delta 的表中,当 P = 2 的时候,查询 K1-K8 时候的切分。在 Figure4 可以看到,Delta#1 查询 btree 深度更大,而 Delta#2 更早停下了。因为算法认为达到了 error margin ratio。当然这个算法也可以往下切,你可以理解成这里的访问是一个 stack 或者 wave,认为某个地方可以切细,就可以访问子节点。
Figure 5 展示了具体切分的效果,这里如果按照估计,总大小上限是 70,假如按照 Figure 5,算法在 K4-K5 之间切分,那么根据算法可以算出每个 Partition 的 min-max 大小。如 Figure5.
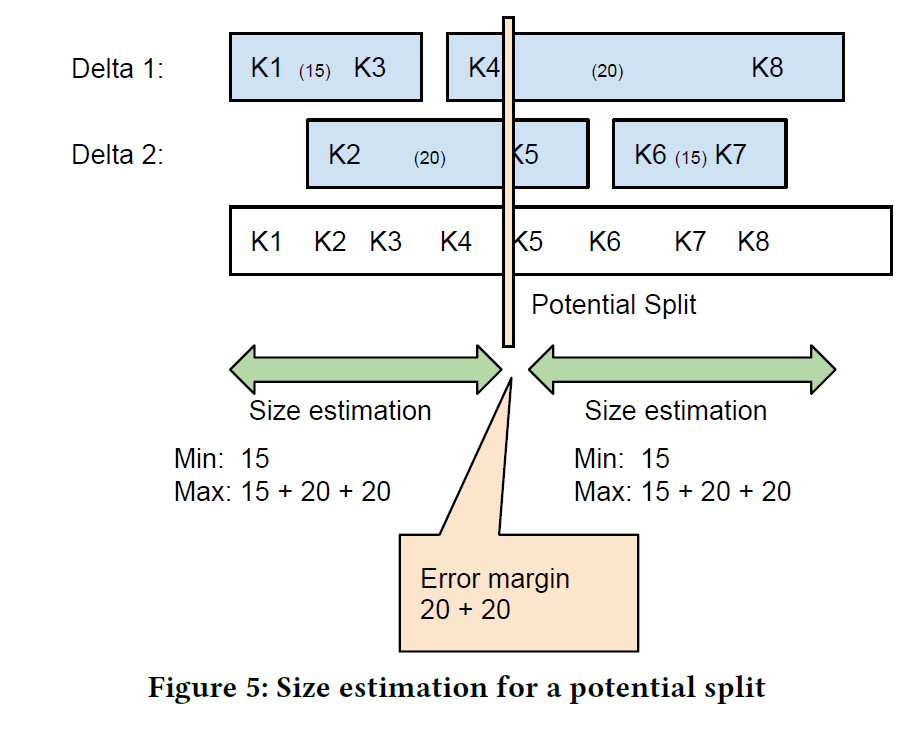
Margin Ratio 可以按照 (Max - Min ) * 2 / (Max + Min) 来计算。如果两个 Partition 比率合理,那么 theta 被视为足够好了,否则算法会访问 btree 的深层来捞统计信息。比如把 [K4, K8] 索引再探深一层(Napa 称这种操作为 Drill Down)
Drill Down 只是部分的
Note that we only need to drill down entries contributing to the error margin. The other entries are kept in the working set (called the set) without matching entry drill down.
但我不知道这个 Contribute 是怎么判定的。。。Margin Ratio 大小合适度又是怎么判定的。。。这些都会在算法细节部分介绍!未完待续!
算法细节
假定 Delta 为 ,第 i 个查询为 。给定查询 Q, 中满足要求的条目称为 mathing entry set . 那么在查询中也可以找到一组满足要求的 。对于每个 B-tree 节点,这里可以找到子条目 和 ,每个条目的 size 等级于自己子部分内容的 size 和。它的统计信息可以简化为 e = <start, end, size, level, block>,[start, end) 代表 key-range. level 代表可以 dive 的层数(我理解层数应该是 hidden 的,不用存,只是个抽象?),e.block 是 child index block 的数量。
算法会逐渐推进,从一个 (virtual) root entry 扩展开来,每次到一层可以更新一批 matching entry set,相当于通过 IO (和部分 CPU 与维护成本)来提供更精细的统计。这里提供的内容基本上是 maximum size estimate。这个精细化的过程就是 DrillDown:
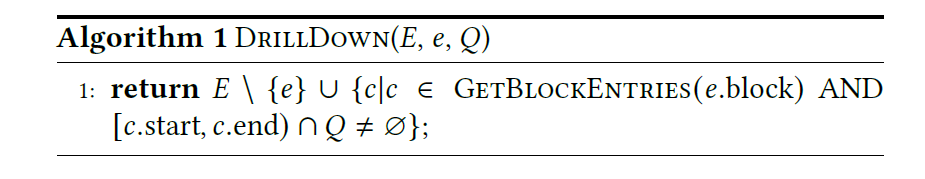
DrillDown 本身可能引入 IO(老实说我感觉 btr 这个东西本身就很容易缓存,但是这种大规模查询可能缓存命中率也做不到很高,具体得测测或者结合 RocksDB Index 的经验看看)。所以这里可能会 Batch 访问下层来优化(说实话我真不懂这了。。。虽然我看着懂他的意思,但是脑部不出为啥要这么写)
Split point candidates
下面是到一组 Entry Sets 里面寻找所有的 bonadry-key 和对应的 cumulative 大小和. 这里希望这里面的切分能够尽量均匀. 在这里 和下一个 key 中间的某个 key 被称为 i split point candidate 。选作中间某个 key 是一个 short-key 优化(类似处理 min-max 过长时候的优化)。
实现上有点类似 DP,会选取<从零到这个这个key 的 size可能的最小>和<从零到这个这个key 的 size可能的最大>。这个说法有点抽象,截图论文了

下面是具体的参数:

通过这个粗糙的计算 size 和错误率。这个问题等价于在所有 m 个 key 中切出 P 个 Paritition(P-1 个 split point)。
下面是找到具体的 split point。本质上是一个 uniform partition 算法。算法的目标是,给定计算.因为这里有一个总大小(相当于最后一个 的 max),所以根据总大小能推断出每个 Partition 的推荐大小。然后扫出一组 Partition,他这里算法我没看懂,复杂度如下

然后这里再次计算 是否足够好了,下面挑选出对应的不合法集合:

这里根据不合法的集合尝试找到需要 dive 的 entry

可以看到,entry 是针对 key 而言的,这里可以针对 key 找到一组对应的需要切的 entry,然后尝试切一下。(论文描述了两种切分方法)
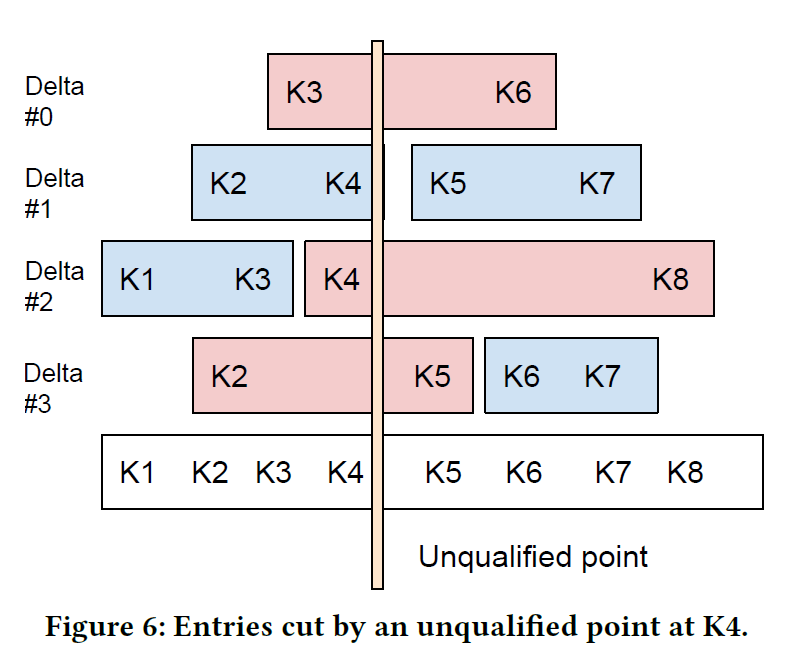
组合起来算法如下:

工程上这里有一些优化:
- 允许用户设置 dop,但是每个 dop 有最小大小限制,用户可能瞎几把设,不能搞太细
- 允许根据 Scan 的 size 来估计,而不是根据 dop 来估计。因为可能 scan size 对于查询估计来说是个更好的东西