Notes on Btree Implements: PostgreSQL

PostgreSQL 也有索引和 BTree 索引，但是它和 InnoDB 是有区别的，InnoDB 有 “Cluster Index”，索引指向 Cluster Index，Cluster Index 上数据有是完整的，它也有 roll_pointer 字段指向 Undo。PostgreSQL 没有 Cluster Index。它的主数据存储在一个叫 Heap Table 的”堆表”上，需要更新的时候，堆表上会插入对应的 Tuple，如果是字段更新，那么会在之前的 Tuple 记录一条指向现有 Tuple 的指针。这里对应的逻辑视图如下：

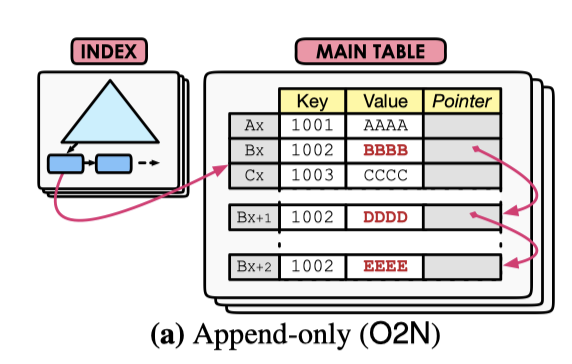
190D2463-5889-453A-8310-C1C1058911D5

也就是说，对比 InnoDB，PostgreSQL 相当于 只有 secondary index。

概念介绍

Tuple

PostgreSQL 的 Tuple 分为 HeapTuple 和 IndexTuple，HeapTuple 是主表上的数据，IndexTuple 是索引上存储的指向 HeapTuple 的数据，它们大致逻辑内容如下：

fig-5-02

fig-5-03

HeapTuple 定义在 pg 的 src/include/access/htup.h, 除了用户定义的值，它包含几个隐藏字段：

  1. t_xmin, t_xmax: t_xmin 表示创建这个 Tuple 的事务的事务 id，即这个事务 commit 之后，事务 id 比 t_xmin 大的就可以看见 tuple ；t_xmax 表示更新或者删除这条记录的事务的 id（它也可以表示事务正在对这个 tuple 上锁）
  2. 实际上，读一个 tuple 的时候，PG 可能要判断一下这个事务 id 的状态是什么样子的，Tuple 的隐藏字段有一些 info bits，如果查完可以把相关状态在 info bits 上做标记，优化查表的开销
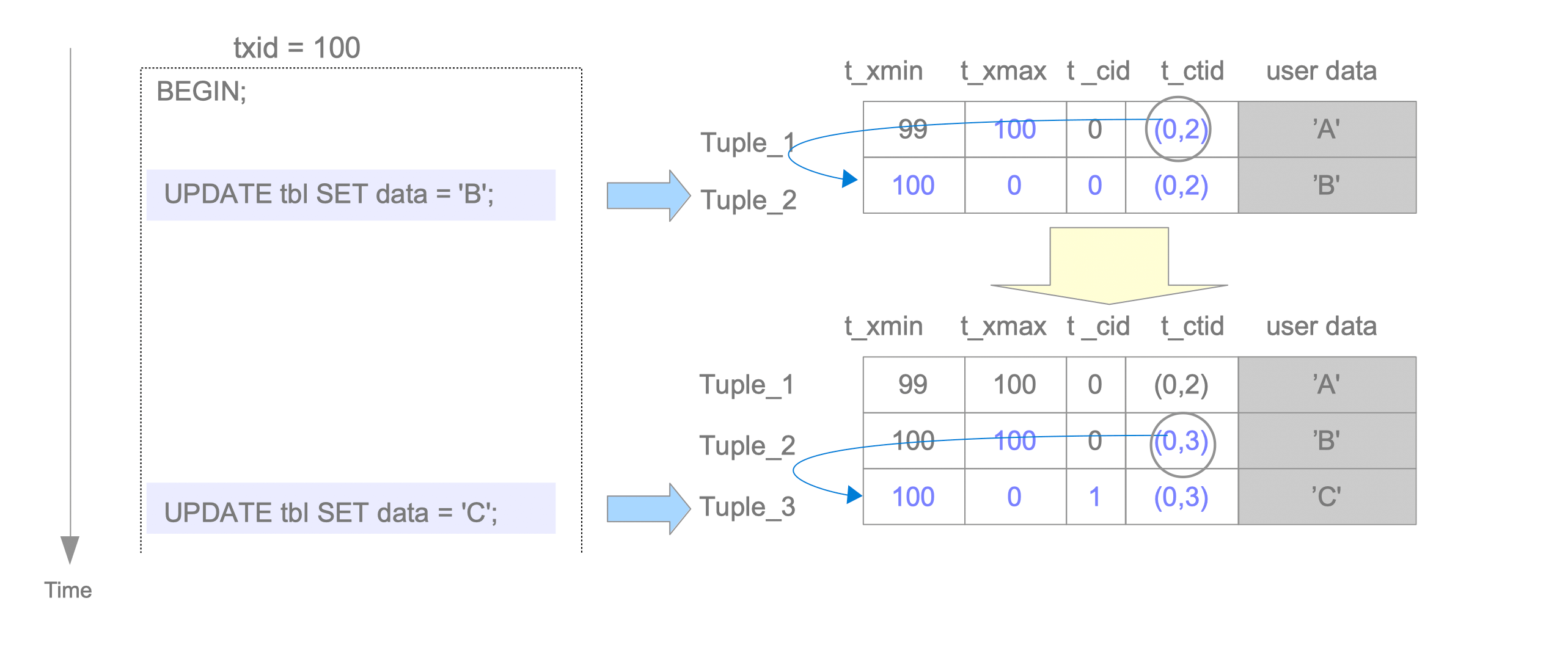
  3. t_cid 是更新这个 tuple 的 command id
  4. t_ctid 是一个指针，指向 Tuple 自己的位置 或者 被更新之后，Tuple新的位置

我们以上图为例：

  1. Page 的 tuple1 被 txn_id 为 99 的事务插入，它的 t_xmin 为 99，t_ctid 指向自己的位置 (0, 1)
  2. Page 的 tuple1 被 txn_id 为 100 的事务更新，它的 t_xmax 为 100, 创建了一条新的记录 Tuple2，t_xmin 为 100，t_xmax 为 0。Tuple1 的 t_ctid 指向 tuple2

对于 IndexTuple，假设主表属性是 (a, b, c), 而对 (b) 建了索引，那么索引 Tuple 可以被视作 <(b), 主表上 Tuple 的位置>, 同时，索引的 IndexTuple 可能只有叶子结点上才有主表 Tuple 的位置。 它被定义在 src/include/access/itup.h

fig-5-06

Page

PostgreSQL 的 Page 格式比较统一，而且非常典型，典型到很多数据库教材上都有。相比 InnoDB 的 稀疏索引 + 单向链表 + 垃圾链表 + 统计信息，PostgreSQL （以降低更新性能为代价）使用了一个非常简单的格式：

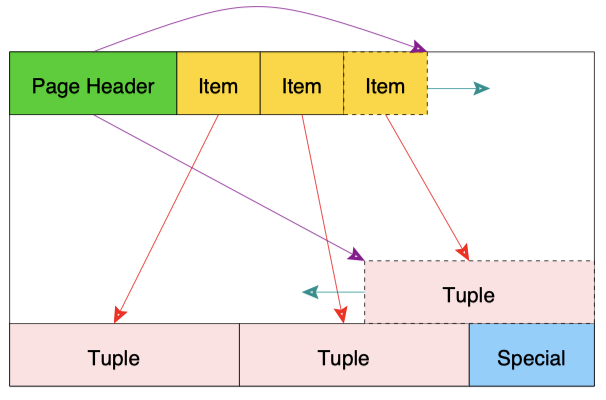
4C345186-B4D8-435E-9C5B-DDD4D18671A5

对于 Heap Table，不考虑 GC 数据（即 Vacuum）的情况下，数据几乎是只会往后添加、不会变更位置的。

Index

终于讲到我们今天的主题了…其实还没有。我们刚才说过，不考虑 Vacuum 的情况下，数据几乎只会往后添加、不会变更位置。Index 需要指向最初的那个 Tuple，如图所示：

PostgreSQL 把 Index 接口和 Index 管理器暴露给了用户，用户可以创建 HashIndex, Btree Index 等索引。

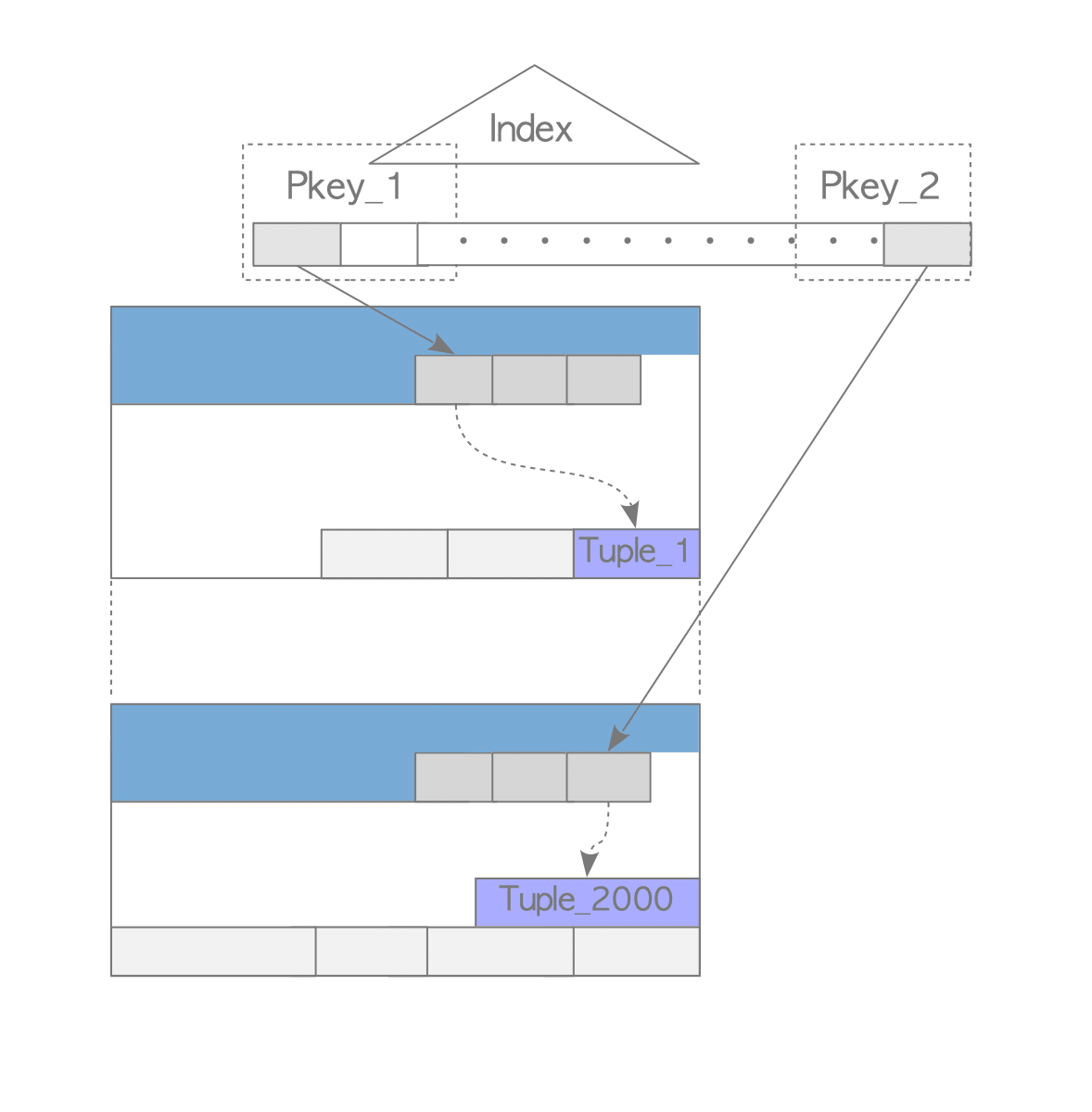
fig-5-14

我们刚才谈到了，更新一个值可能会更改它的 t_ctid，指向新的位置。这个时候 索引的值不能改变，同时旧值不能被回收，除非索引相关的值被改变。如果 Tuple 为 (a, b, c), 对 (b) 构建了索引，然后一个请求修改了 b，这个时候需要在索引插入一个新的值，但旧值也不能删除。需要等待 vacuum 阶段删除。

Vacuum

对于 PG 来说，它做的是一个比较复杂的多阶段的删除，用的 Tuple-level GC + VAC，具体可见 Vacuum 相关的材料（Lazy Vacuum, Full Vacuum）

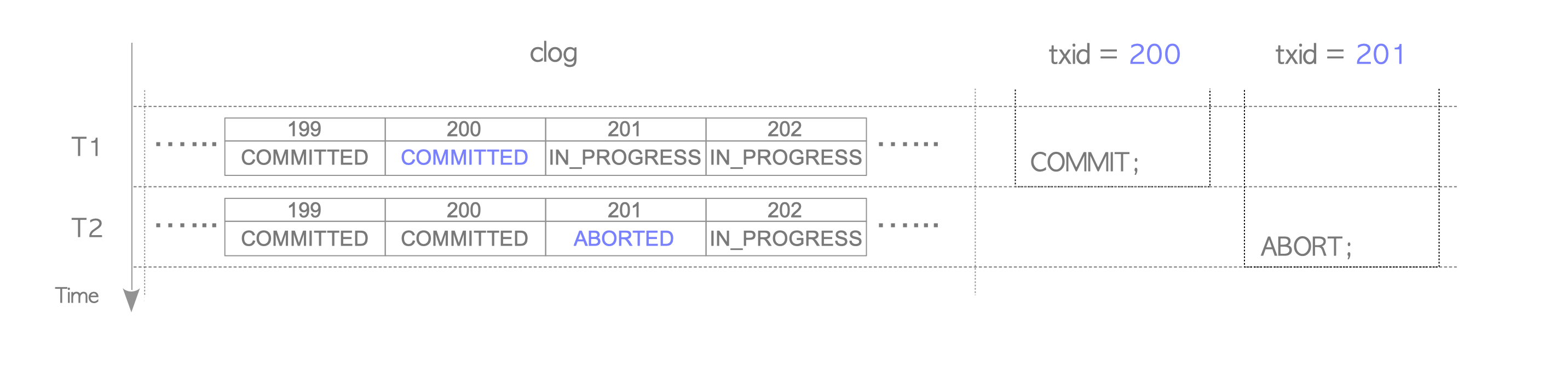
  • 对于事务的记录，PostgreSQL 维护在 clog 里面，这可以当作一个事务表。它根据事务 id 的顺序存在各个 Page 上，缓存在内存的 slru 中。当事务推进的时候，可以 Truncate 前面的事务记录来回收空间，推进系统事务
  • PostgreSQL 的 xmax 如果被标记且 tuple 没有被上锁，那么这个 tuple 是被删除的，如果 xmax 小于 min-txn，那这个 tuple 在逻辑上不会被任何事务看见，虽然物理上它还存在
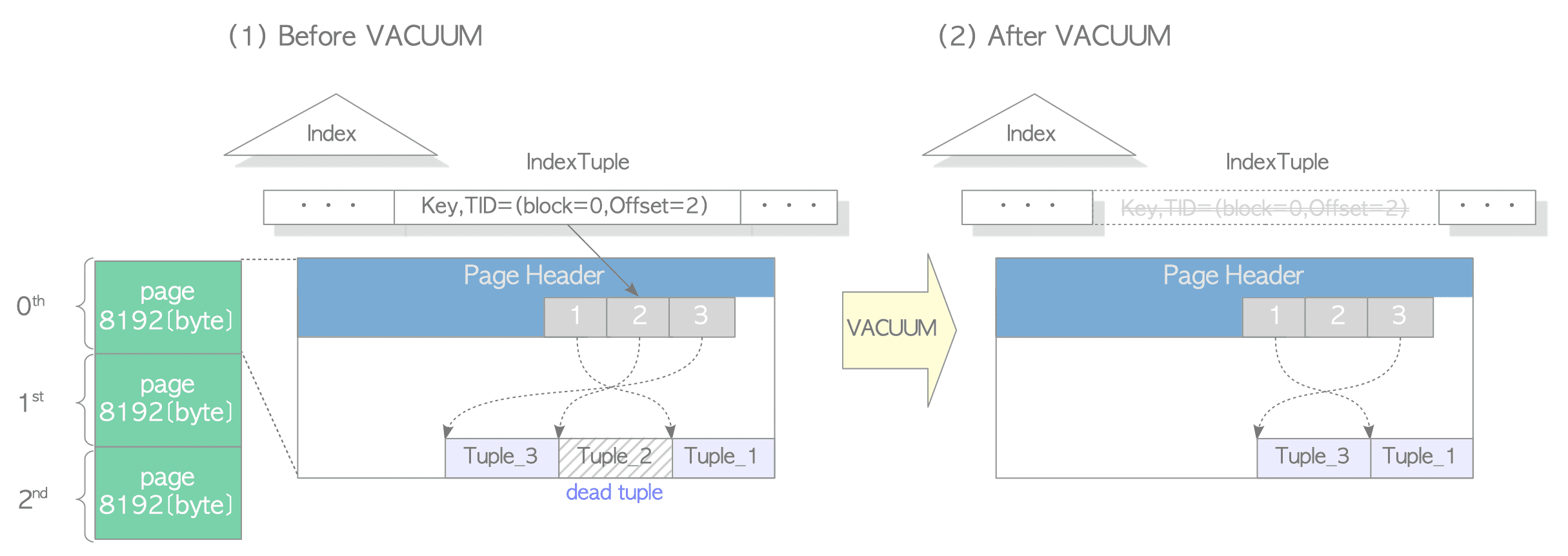
  • GC 过程中，PostgreSQL 会扫描所有 dead 的 tuple，然后清除它们，这里首先有一个 visibilitymap, 对应代码在 backend/access/heap/visibilitymap。如果某个 Page 被改了，有 Tuple 可能需要 GC，就会给 vm 记一下，然后这样的 Page 才需要被清理，这段过程中，索引的数据会被清除，如下面的图。
  • 索引数据清除之后，Heap Tuple 的数据会被标记删除，但是 slot 上的位置还是会留着。
  • 更新对应的 VM，移除 clog 等事务表信息。

fig-6-01

事务状态: CLOG

fig-5-07

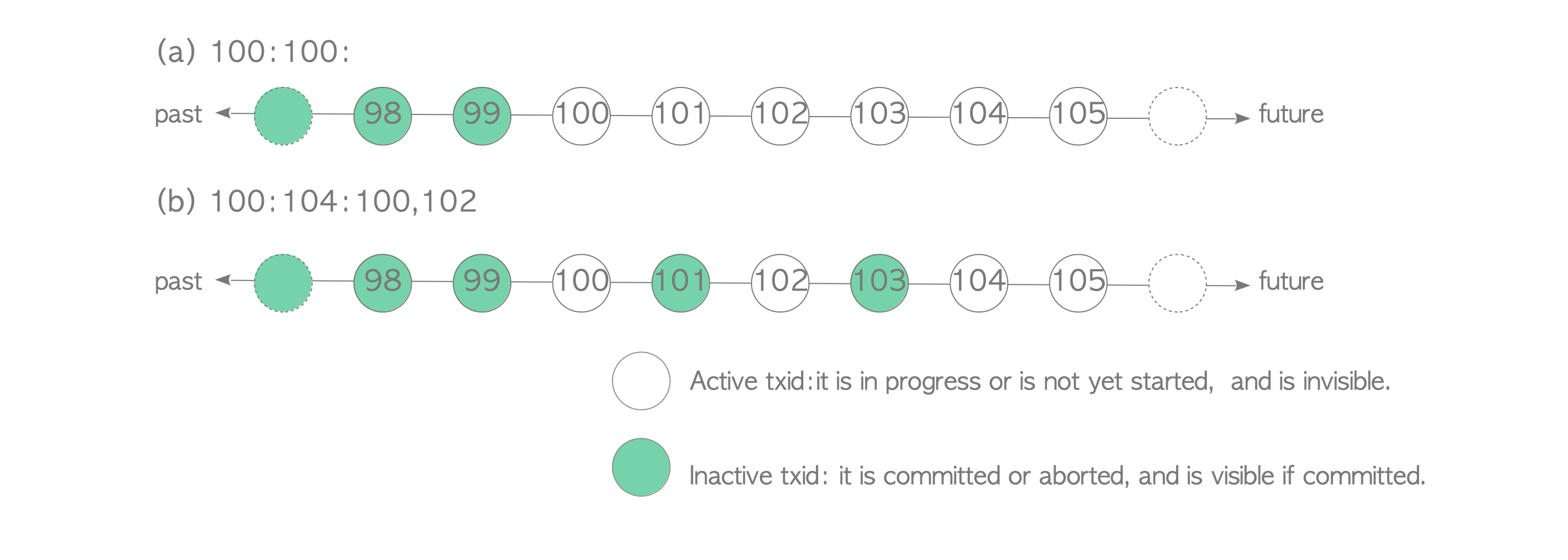
fig-5-08

WAL: XLog

PostgreSQL 的日志写在 XLog 中。PostgreSQL 模型中，没有 InnoDB 的 Undo data，但它认为它在 Heap Table 中维护了多版本，所以只写了 Redo Log。

NBTree

PostgreSQL 的索引管理器定义在了 src/backend/access/index，而 Btree 的定义在 src/backend/access/nbtree。BTree 对外提供了 cursor, 插入，删除等接口，同时也定义了并行访问的接口。

PostgreSQL 实现了 B-link Tree，B-link Tree 来自论文 Efficient Locking for Concurrent Operations on B-Trees 逻辑定义如下：

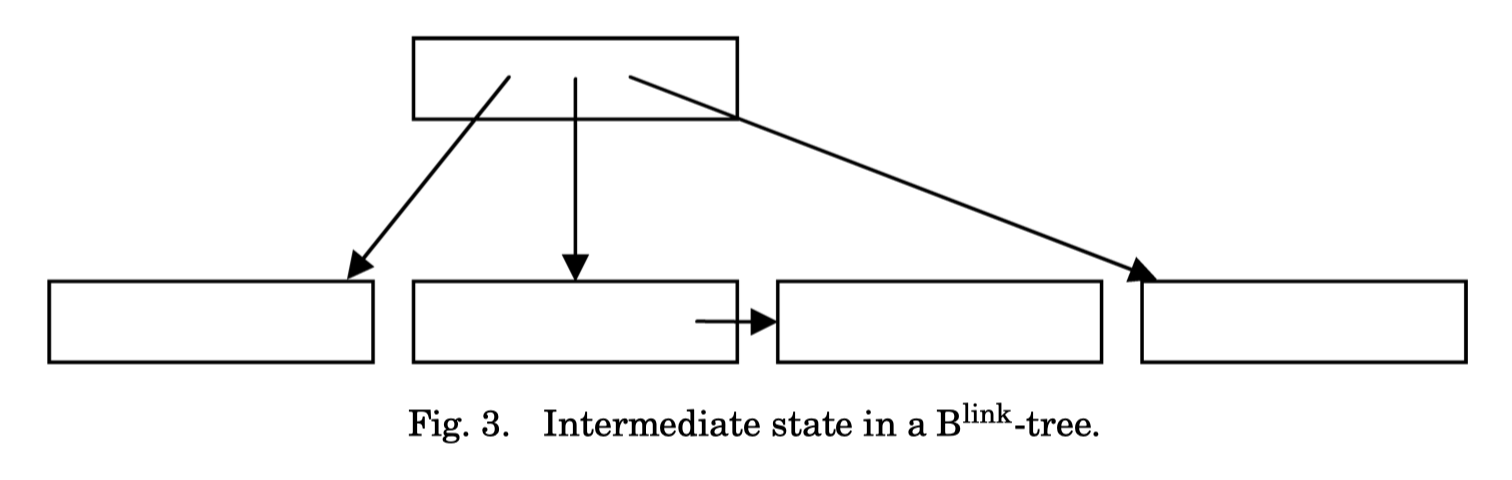
68DC4BF6-FEDB-47B0-A10E-A981B22BECC3

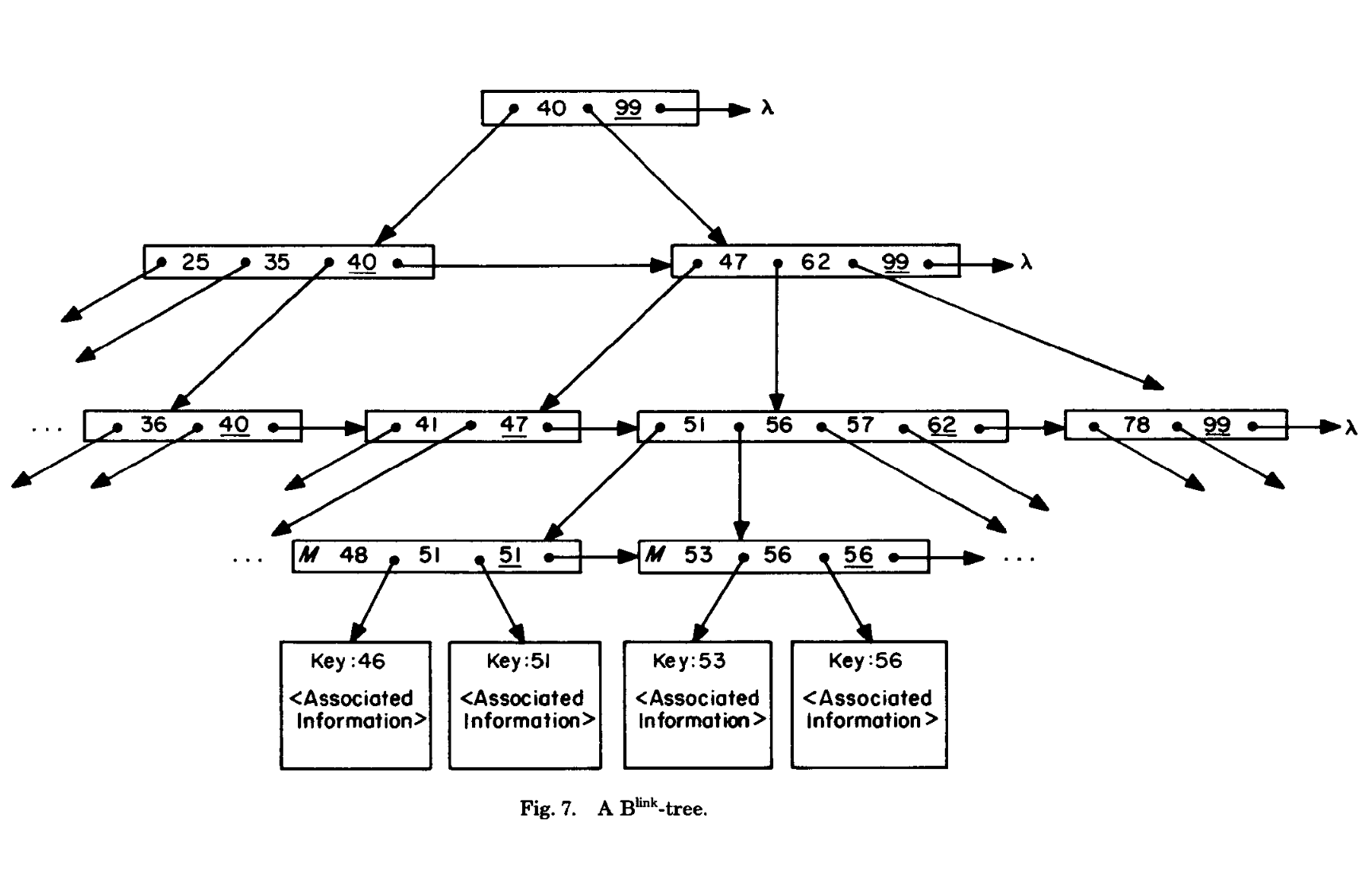
AD6DE068-6D32-4756-8ED3-E841A8969781

  • 所有页面可能包含一个 highkey，表示本页面存储的 key 的最大值。同时可能包含一个分裂到一半需要的 rightlink，指向自己节点的右边。比 highkey 高的值可以去右边查询，走到右边的行为叫 moveright
  • b-link tree 的分裂是分为多阶段的
    • 分裂的时候，永远只会向右分裂，首先节点会创建一个右节点，修改 high-key，链接 rightlink，完成操作的第一步
    • 之后发现这里有未完成的分裂后，会在父节点上插入右节点，完成分裂。如果父节点分裂，那么回到上一步，递归完成分裂。

对于一个下降的查询 key，它移动下来的时候，会先比较 key 和 这个 Page 上的 highkey，如果自己小于 Page 的 highkey，那么就在本页面查询，否则会需要 moveright，移动到右节点查询。

PostgreSQL 的 Index 对外暴露了一组管理 api，包括：

  1. Search
  2. 插入节点
  3. 更新一些节点的元信息
  4. Scan
  5. Batch 的在 vacuum 阶段做删除节点
  6. …

在 Datum bthandler(PG_FUNCTION_ARGS) 这个函数有着将函数 bind 到 IndexAm 上的逻辑。这里其实基本上相当于虚函数什么的了。

BTree 的结构和各种Page

我们在刚刚介绍 InnoDB Btree 的时候提到过，InnoDB 有整个索引的锁，同时它的 RootPage 是不会改变的。

InnoDB 的 RootPage 是会改变的，它有一个 MetaPage 指向它。Meta 永远是整个树的第一个 Page，而 Root 和 Internal Page 其实没有什么区别。如下图：

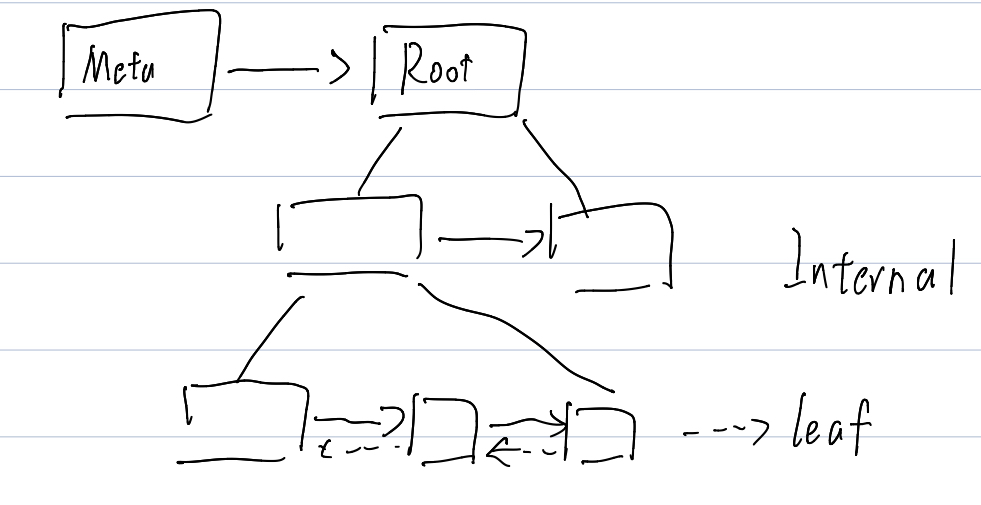
IMG_1042

还可以注意到，Leaf Page 是有左指针 leftlink 的，这是因为反向 Scan 的时候，它希望不获取上层 Page 直接 Scan 下来。

BTree 相关的内容定义在 src/include/access/nbtree.h，我们可以从 Meta 看起：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
 * The Meta page is always the first page in the btree index.
 * Its primary purpose is to point to the location of the btree root page.
 * We also point to the "fast" root, which is the current effective root;
 * see README for discussion.
 *
 * MetaPageData 指向
 */

typedef struct BTMetaPageData
{
	// 一些标志位
	uint32		btm_magic;		/* should contain BTREE_MAGIC */
	uint32		btm_version;	/* nbtree version (always <= BTREE_VERSION) */
	
	// 真实的 root
	BlockNumber btm_root;		/* current root location */
	uint32		btm_level;		/* tree level of the root page */
	
	// Fastroot 相关的内容
	BlockNumber btm_fastroot;	/* current "fast" root location */
	uint32		btm_fastlevel;	/* tree level of the "fast" root page */
	/* remaining fields only valid when btm_version >= BTREE_NOVAC_VERSION */

	// 一些 vacuum 有关的标记.

	/* number of deleted, non-recyclable pages during last cleanup */
	uint32		btm_last_cleanup_num_delpages;
	/* number of heap tuples during last cleanup (deprecated) */
	float8		btm_last_cleanup_num_heap_tuples;

	bool		btm_allequalimage;	/* are all columns "equalimage"? */
} BTMetaPageData;

上面是整个 Page 的信息。

对于 Internal Page 和 Leaf Page，PostgreSQL 并没有引入额外的结构，它和我们之前聊的 Page 结构是一样的，只是 Tuple 是 IndexTuple，尾部内容如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/*
 *  在 Page 的尾部, 存储 Page 的 left 和 right 的兄弟节点和 btree 的 level,
 *   page 的 type. Vacuum 本身也会占有锁.
 *
 *	BTPageOpaqueData -- At the end of every page, we store a pointer
 *	to both siblings in the tree.  This is used to do forward/backward
 *	index scans.  The next-page link is also critical for recovery when
 *	a search has navigated to the wrong page due to concurrent page splits
 *	or deletions; see src/backend/access/nbtree/README for more info.
 *
 *	In addition, we store the page's btree level (counting upwards from
 *	zero at a leaf page) as well as some flag bits indicating the page type
 *	and status.  If the page is deleted, a BTDeletedPageData struct is stored
 *	in the page's tuple area, while a standard BTPageOpaqueData struct is
 *	stored in the page special area.
 *
 *	We also store a "vacuum cycle ID".  When a page is split while VACUUM is
 *	processing the index, a nonzero value associated with the VACUUM run is
 *	stored into both halves of the split page.  (If VACUUM is not running,
 *	both pages receive zero cycleids.)	This allows VACUUM to detect whether
 *	a page was split since it started, with a small probability of false match
 *	if the page was last split some exact multiple of MAX_BT_CYCLE_ID VACUUMs
 *	ago.  Also, during a split, the BTP_SPLIT_END flag is cleared in the left
 *	(original) page, and set in the right page, but only if the next page
 *	to its right has a different cycleid.
 *
 *	NOTE: the BTP_LEAF flag bit is redundant since level==0 could be tested
 *	instead.
 *
 *	NOTE: the btpo_level field used to be a union type in order to allow
 *	deleted pages to store a 32-bit safexid in the same field.  We now store
 *	64-bit/full safexid values using BTDeletedPageData instead.
 */

typedef struct BTPageOpaqueData
{
	/** 两个兄弟 **/

	BlockNumber btpo_prev;		/* left sibling, or P_NONE if leftmost */
	BlockNumber btpo_next;		/* right sibling, or P_NONE if rightmost */
	// 本 tree 的深度
	uint32		btpo_level;		/* tree level --- zero for leaf pages */
	// 下面几行就介绍这些 flags 了
	uint16		btpo_flags;		/* flag bits, see below */
	BTCycleId	btpo_cycleid;	/* vacuum cycle ID of latest split */
} BTPageOpaqueData;

这里我们关注 btpo_next，是对应的下一页。这是一个定长的字段。那么 highkey 存在哪里呢？答案是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 *	Lehman and Yao's algorithm requires a ``high key'' on every non-rightmost
 *	page.  The high key is not a tuple that is used to visit the heap.  It is
 *	a pivot tuple (see "Notes on B-Tree tuple format" below for definition).
 *	The high key on a page is required to be greater than or equal to any
 *	other key that appears on the page.  If we find ourselves trying to
 *	insert a key that is strictly > high key, we know we need to move right
 *	(this should only happen if the page was split since we examined the
 *	parent page).
 *
 *	Our insertion algorithm guarantees that we can use the initial least key
 *	on our right sibling as the high key.  Once a page is created, its high
 *	key changes only if the page is split.
 *
 *	On a non-rightmost page, the high key lives in item 1 and data items
 *	start in item 2.  Rightmost pages have no high key, so we store data
 *	items beginning in item 1.
 */

#define P_HIKEY				((OffsetNumber) 1)
#define P_FIRSTKEY			((OffsetNumber) 2)
#define P_FIRSTDATAKEY(opaque)	(P_RIGHTMOST(opaque) ? P_HIKEY : P_FIRSTKEY)

我们可以给 Page 画一个草图，如下：

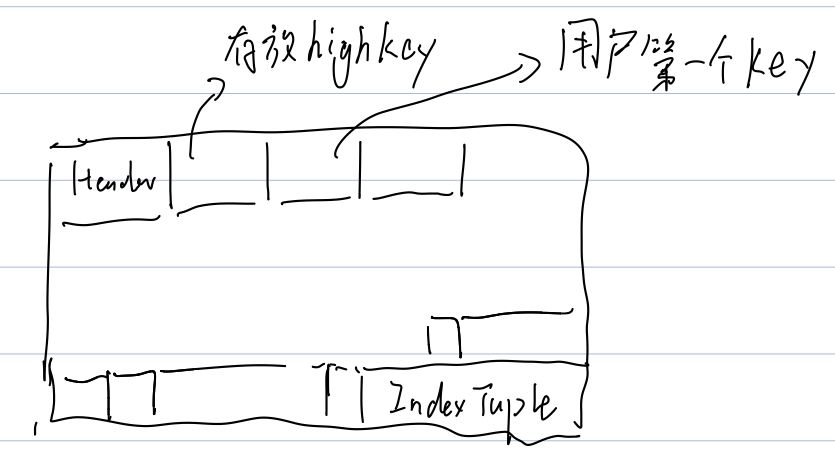
E586E76B8C150D42A8D7A4AA738ACB98

此外，需要注意，对于 Internal Page 用户的第一个 key 相当于 -inf，它小于任何一个值。具体可以参考 _bt_compare 的注释。

在叶子结点上，IndexTuple 包含有指向的 HeapTuple 的位置。

Fastroot

我们可以看到, MetaPage 有一个 fastroot，这个地方表示的是实际逻辑上的 Root，如下图：

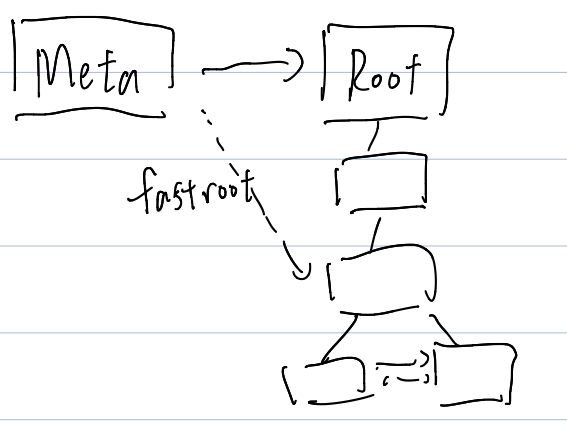
C0C2426A8807D6CA2DB200A68939625B

这里 Root 到很下层都只有一个 link（可能是由于分裂和删除导致的，为什么会形成这种结构之后会讲），所以真实的 root 不等于访问上最快捷的 root，Meta 会有个 fastroot 来指向开始分叉的结点，来优化读

Btree 的查找和移动

下降

Btree 下降的主要逻辑在下列两个函数：

1
2
3
4
extern BTStack _bt_search(Relation rel, BTScanInsert key, Buffer *bufP,
						  int access, Snapshot snapshot);
extern Buffer _bt_moveright(Relation rel, BTScanInsert key, Buffer buf,
							bool forupdate, BTStack stack, int access, Snapshot snapshot);

一个下降，无论是插入还是查找，都会走到 _bt_search，不过这两种情况的 access 标识是不一样的。读取的时候，access 是 BT_READ, 写入的时候是BT_WRITE 。Relation 是整个关系（可以理解成表，有 HeapTable 和 Index 的信息），BTScanInsert 是需要查找的或者插入有关的 key，他可能会指定是否是 next_key, 查询的方向等。最后会搜到叶子结点，返回 BTStack，即 Btree 遍历的时候的栈。

我们首先介绍读的下降，下面逻辑对应的逻辑都在 _bt_search 中，假设第一次到第 k 层

  1. 拿到本 Page 的读锁，对本 Page 进行 Pin。比较本 key 和 Page 的 highkey。如果小于等于 highkey，那么可以继续下降，否则，需要 _bt_moveright 向右移动
  2. 向右移动的时候，先拿到右 Page 指针，然后再释放锁和pin，再 acquire 右边的 Page 和锁，然后回到 (1) 的逻辑
    1. 正确性：释放锁后，本 Page 和右边的 Page 可能都会分裂，因为 highkey 的限定，本 Page 分裂后，所有值仍然小于 highkey。而右边 Page 如果分裂，也只会向右分裂。Page 可能会删除 Page，这个时候删除 Page 的并发逻辑会保证删除的正确性
  3. 如果移动到了 key <= highkey 的场景，那么我们就找到了，如果是叶子结点，那就访问叶子，否则下降。这里首先把这个节点放到 BTStack 这个遍历的栈中，然后查找到走哪个 key 下降（调用 _bt_binsrch 做二分查找），然后释放自己的锁和 pin，再下降，这里仍然是靠 highkey 保证了下降的正确性。

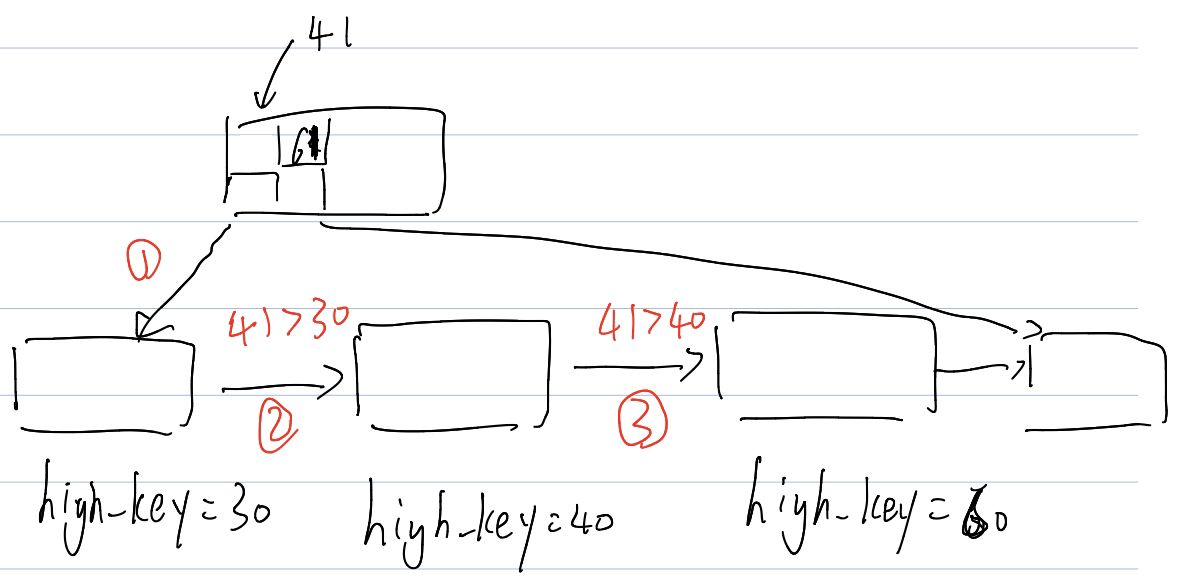
60C70C6E4770D882C1A15954F931DADF

这里就可以正确的到达了。然后上面是讲第 k 层下降的。那根结点是怎么拿到的呢？这里会拿到 fastroot，直接下来就行了。用户没有插入任何值的时候，root 可能不存在。PG 如果发现 root 不存在，那就会直接返回 “啥都没查到”。

对于插入而言，如果没有 RootPage，会创建一个 RootPage。插入的逻辑从 _bt_doinsert 开始，Btree 会在 Relation 上记录最右 Page，如果 Page 是一个最右插入（即大于所有的插入值），那么它会直接走到最右侧的 page, 把它当作 root (记得吗，root 只是一个正常的 internal 或者 leaf page), 否则，它会返回树的 root。如果是插入的话，PG 发现 root 不存在，会直接创建一个 Root。

接下来，它会走 _bt_search，这里大概逻辑和 1-3 是一样的。不过读的时候拿的从根到叶子都是读锁，但 写在叶子结点的时候会切成写锁。

还有一些地方有区别，在写链路上，这里如果遇到了未完成的分裂，会驱动父节点把 rightlink 完成分裂，插入父节点。这部分代码在 _bt_moveright 和 _bt_finish_split 中。

Scan

PostgreSQL 的 Scan 会首先下降到叶子节点，然后向右或者向左进行迭代。Scan 相关的一组函数如下：

1
2
3
bool _bt_first(IndexScanDesc scan, ScanDirection dir); // 找到第一个对应位置, 然后把结构存在 `scan` 里面
bool _bt_next(IndexScanDesc scan, ScanDirection dir);  // 对 scan 捞到下一个值
bool _bt_endpoint(IndexScanDesc scan, ScanDirection dir);

Scan 首先要争取处理方向，然后 IndexScanDesc 描述了 Index 和 ScanKey 的关系：可能是 >=, <=, > , < 等。这里才实际执行的时候会变成：

  1. goback: 是否要回退一个。如果 goback == true，就要回退一项
  2. nextkey: 是否要拿到大于搜索项的 key。这个有点怪，nextkey 设置的时候，会拿到 item > scan key的，否则直接 item >= scan key 就可以了

有点绕，我们可以看看具体分析，这里有：

  1. 如果是 <, 那么会当 >= 处理，然后需要 goback
  2. 如果是 <=，那么会当成 >= 处理，需要 goback + nextkey
  3. …

这里会构造一个搜索的 key 对象，来进行 _bt_search，再走 _bt_binsrch 在页面上定位到对应的位置。

下面会有一些比较 hack 的地方，在定位到位置后，这里会用 _bt_readpage来读出本页面剩下来所有内容，然后释放锁。这个地方感觉有点 RC 的意思了，新插入的数据感觉 PostgreSQL 是读不到的。猜测它这就没在意这个。释放锁是个很奇怪的地方，我们后面会论证它的正确性。

_bt_next 移动到下一个要读的目标。这里有缓存的话，会先读取自己的缓存，没有的话，会走到下一个页面，调用函数: _bt_steppage(IndexScanDesc scan, ScanDirection dir)。

如果要向右移动，这里 PostgreSQL 会在搜到页面然后放锁之前，拿到 Page 的 right link，然后在需要跳转到下一个页面的时候拿到，这里逻辑如下图：

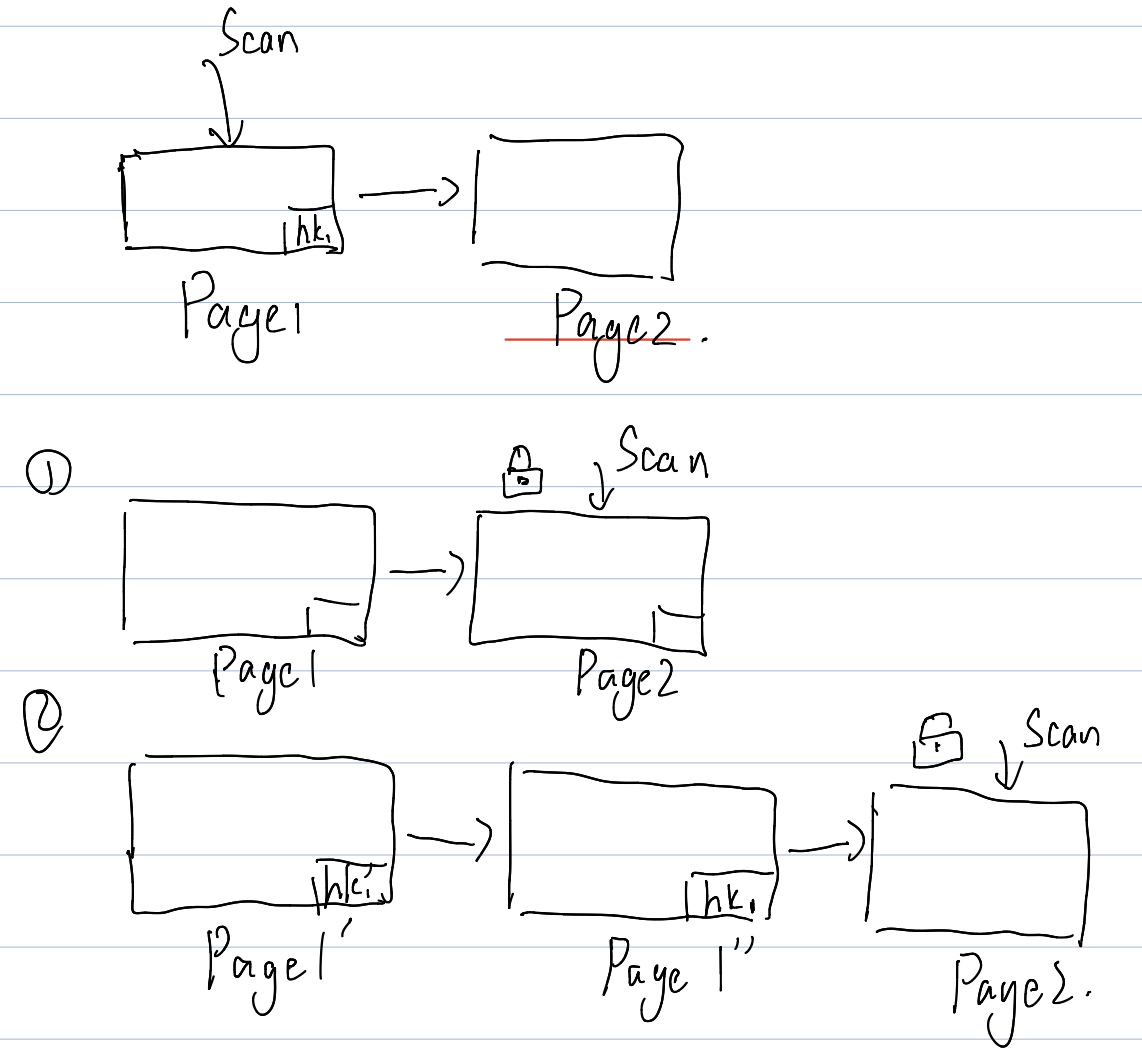
IMG_1046

  1. 如果自己这个 Page 没有分裂，即 (1)，那么移动到正确的页面
  2. 如果自己这个 Page 分裂了，然后这里可以直接移动过去。

读左边的页面比较复杂，需要验证比较多东西。这个时候会：

  1. 先锁住本页面，拿到 left-link，注意，向右移动的时候拿的是刚下来的时候拿到的 right-link, 反之 left-link 则是在需要左移的时候再拿的
  2. 放锁，走 left-link，拿到 left 的页面的锁
  3. 查看右边的 Page 是不是原来的 Page，如果是的话，就成功了，否则要向右再移动

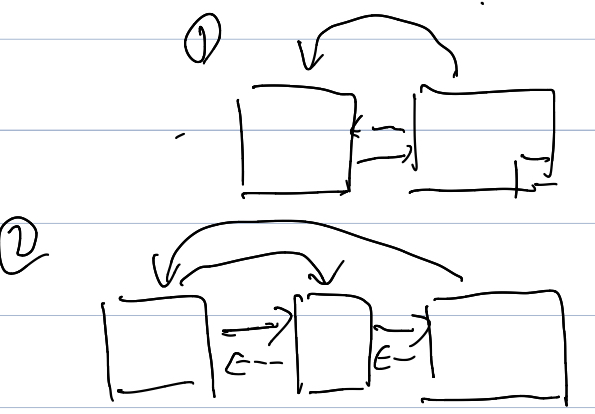
IMG_1047

这里相对右移会复杂很多。这里再额外讨论一个 Page 被删除的情况。这个情况会根据 high key 来判断移动的范围。

插入和分裂

B-link tree 的分裂也是 Btree 的分裂，和 InnoDB 一样，PostgreSQL 也支持按照 bytes 50%-50% 分裂，也能支持向右分裂。我们这里可以先看看插入的时候用的栈：

1
2
3
4
5
6
7
btinsert -- hook 在上层插入的函数
- _bt_doinsert -- 转换了一下 key, 具体的去做 insert
  用我们上面介绍的逻辑, 走 _bt_search_insert, 里面会走我们上面的逻辑, 需要注意的是, **这里检测到未完全分裂的 Page, 会做 _bt_finish_split, 完成分裂**
  做一些 checkUnique 和事务有关的东西(比如上锁), 可能会走到 HeapTable 上验证, 或者靠 LP_DEAD 等辅助位判断
  - _bt_insertonpg, 具体插入
  如果 PageGetFreeSpace(page) < itemsz, 调用分裂, 走 _bt_split 和 _bt_insert_parent
  否则, 直接插入页面, 写一条 xlog, 然后标识 LSN.

这里在搜索的时候，会有一些特殊的逻辑，搜索路径上碰到分裂会做 _finish_split

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*
 * If this page was incompletely split, finish the split now.  We do
 * this while holding a lock on the left sibling, which is not good
 * because finishing the split could be a fairly lengthy operation.
 * But this should happen very seldom.
 */
if (P_INCOMPLETE_SPLIT(opaque))
{
	_bt_finish_split(rel, rbuf, stack);
	rbuf = InvalidBuffer;
	continue;
}

if (!P_IGNORE(opaque))
	break;
if (P_RIGHTMOST(opaque))
	elog(ERROR, "fell off the end of index \"%s\"",
		 RelationGetRelationName(rel));

第一阶段: 页面分裂

页面分裂会带上锁，然后把页面分裂成两份，然后标记页面为 unfinished split. 代码逻辑在 _bt_split:

  1. _bt_findsplitloc 找到分裂点。这里准备临时的 leftpage 和 rightpage 作为目标，rightpage 需要持久化到存储中，leftpage 会写回原来的 page1
  2. 产生新 Page, 在内存申请 page， 设置写入的 LSN，寻找分裂到左边的 highkey 等
  3. 用 _pg_addtup 插入元素。
  4. 写 xlog，把两边的更新写入 log buffer, 然后重新设置 LSN.
  5. 放锁

第二阶段: 插入父节点

_bt_finish_split 在扫描阶段会检测到分裂到一半的节点，他会判断自己是不是 root，对自己和右节点上写锁（下降的时候，需要释放读锁，然后切成写锁），然后走 _bt_insert_parent，而分裂在代码上也会走 _bt_insert_parent。这里会有叶子和兄弟阶段的写锁。

_bt_insert_parent 中，之前 BTStack 上的锁都释放了，这里父节点不能被删除（因为删除比较特殊），但可能分裂了，所以要查到真的父节点在哪，然后再插入。插入很简单，但是查找父节点比较 hack，这部分代码在: _bt_getstackbuf:

  1. 找到 stack 的父节点，get 起来然后捞到死锁
  2. (递归的) 调用 _bt_finish_split, 完成 incomplete split.
  3. 扫描 page，看看子节点有没有对应的待完成分裂的那个，如果有的话，搜索成功
  4. 否则，尝试 moveright

Root 的分裂

根节点的分裂和正常节点没有什么区别，这里根分裂会产生一个新的根节点，然后让 meta 指向它。

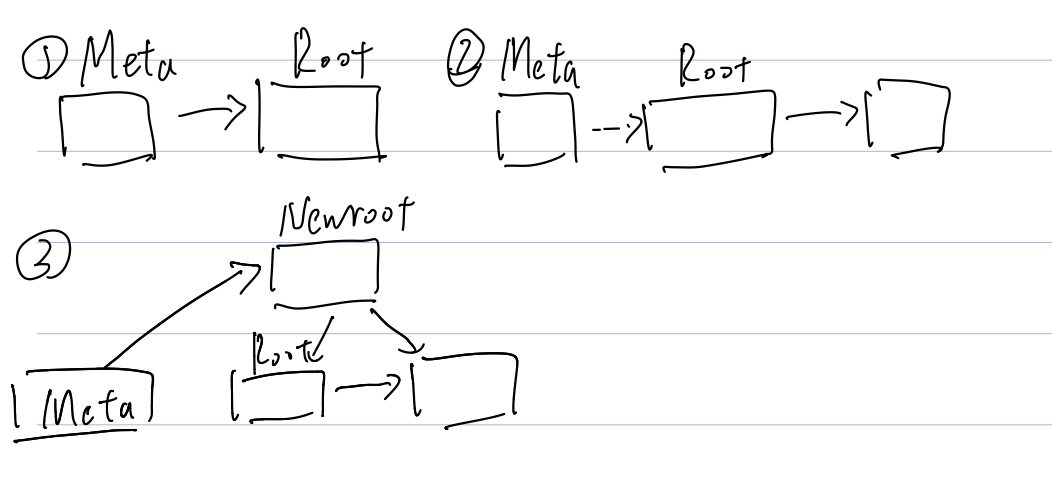
IMG_1048

这里走的逻辑是 _bt_newroot，需要修改 MetaPage 上的标记

对 Key 的删除

在原来的 B-link 树论文中，Delete 几乎是串行的。其实 B-link tree 也差不多，删除会占据 super lock：删的时候，页面要没有 Pin (防止 Scan 出问题) 也要没有 Lock。

PG 不会对 key 简单删除，只会在 vacuum 的时候进行删除。PG 还有一个 simple delete，这里会把 touch 不到的多余的版本标记为 LP_DEAD，等待回收。

PG 只有叶子节点删空了才会被回收，回收也是多阶段的，需要调整兄弟节点的指针，所以非常非常麻烦，这里会先调整指针，然后再把整个子结构摘除。