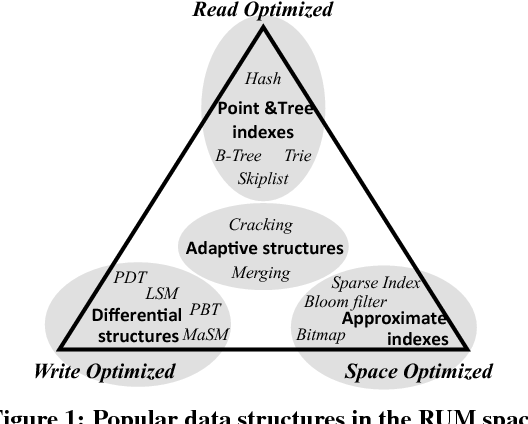
LSM-based Storage Techniques: A Survey

mwish

2021-04-21

如今，LSM-Tree 正在渐渐被大众所接受。或许是从 BigTable 开始，NoSQL 的存储引擎从 DB 教科书上占一大节的 B+Tree，慢慢转向了 LSM-Tree。BigTable, Dynamo, HBase, Cassandra, LevelDB, RocksDB 和 AsterixDB 都使用了 LSMTree 作为存储引擎。

这篇论文简单介绍了 LSM-Tree，然后对读/写/空间相关的内容，对原始论文的 LSMTree 做了分析。同时介绍了 LSM-Tree 相关的的优化。

LSM-Tree 设想是，把所有的、很可能是 随机写 的写入变更存储在内存中，然后转化成顺序写 flush 到磁盘上。LSM-Tree 有下列优点：

优秀的写性能
不俗的空间利用率
比较容易实现的 concurrency control 和 recovery （这在 B-Tree 中比较复杂，设计 btree concurrency control，甚至可能把事务相关的信息嵌入整个 Btree）

LSM-Tree 目前有各种修改，可以适应各种 workload，比如 RocksDB，在它的 FAST21 论文中涉及：

real-time data processing , graph processing, stream processing, and OLTP workloads.

LSM-Tree Basics

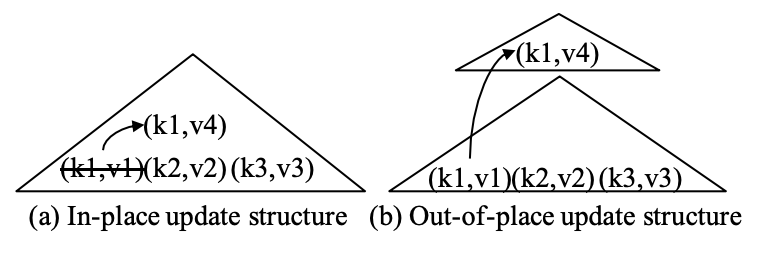
C272EA0D-4077-4696-BE9D-F09734F2C5A3

索引结构有两种更新方式：

In-place update: 就地更新，对写入不是很友好，通常可能只保持需要的版本(论文里说最新的版本，不过我感觉实际上更多是“需要的版本”)，对读和通常比较友好。
Out-of-place update: 对写入比较友好。

1976 年提出的 Different files 是一个比较早期的 out-of-space 更新，维护了一个 diff file 和一个 main file，而 pg 也会把写都记录到一个 sequnce-log 里面，由 vacuum cleaner 进行 GC。类似的思路也被利用到了 LFS 文件系统上。

以上结构大概是维护 log/维护 delta 和 main, 他们的问题是：

low query performance: query 需要根据之前所有的 log 来做出决策
low space utilization: 不需要的内容 (obsolete records) 没有被删除，导致不小的空间放大。

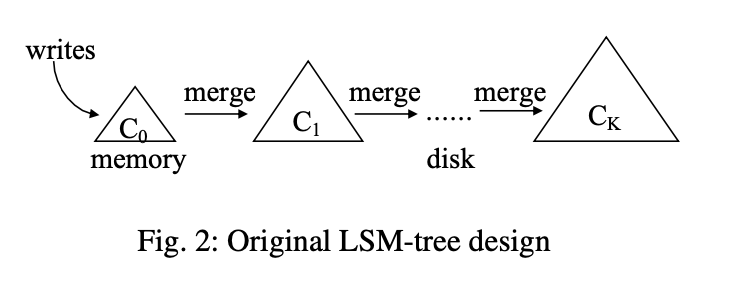
A5D820DF-48C2-40D1-AD32-15FE3C6B228E

最早的 LSM-Tree 在 1996 年提出，如上图。它提供了很高的写性能与不差的读性能。

LSM-Tree 有多个 components，$C0$ 驻留在内存中，其余部分在磁盘上。$C_i$ 状态是 full 的时候，会有一个 rolling merge 进程，把 $C_i$ 的 leaf 刷到 $C{i + 1}$ 中。这个有一点点类似 LevelDB 的 leveling merge，不过：

However, as we shall see later, the originally proposed rolling merge process is not used by to- day’s LSM-based storage systems due to its implementation complexity.

需要注意的是，对于 $Ti = | C{i + 1} | / | C_i|$ 而言，保持一样的比例，会使得 LSM-Tree 写性能有所优化。

差不多同一个时候，Jagadish et al. 提出了一个多层的结构，当 L 层满的时候，会把本层全部内容下刷到 L + 1 层。在如今的 LSM-Tree 中，这种行为被称为 tiering merge policy，即 tiered compaction。

今日的 LSM-Tree

目前的 LSM-Tree 写入的时候，会写一条记录，删除的时候，标志一个 tombstone （类似 leveldb 的 type）。今天的 LSM-Treee 会利用不可变的结构，来简化 concurrency control 和 recovery：merge 的时候，原来的内容不会变更，这与之前提过的 rolling merge 是不同的。

在当今 LSM-Tree 实现中，内存结构通常使用并发的数据结构，比如 SkipList(这种结构比较容易实现 concurrency ordered map) 或者 B+Tree. 在磁盘的结构则使用 SSTable 或者 B+Tree。这里介绍一下 SSTable，它包含多个 data block 和一个 index block, index block 包含了 range 的元信息和 data block 的信息。(可见 BigTable 论文)。

对于 LSM-Tree 的查询有两种：point lookup query 和 range query ，前者从写入时间的新-旧，一个个结构找，直到找到对应的内容或者 miss, range query 则需要一个类似 priority queue 的内容，来吐出对应的 key。以上可见，对于写入增加 —> 磁盘结构变大、层数变多，这里查找的性能是会下降的。Compaction 会以写来优化读和空间放大，目前有两种常见的 Compaction:

tiered compaction
leveled compaction

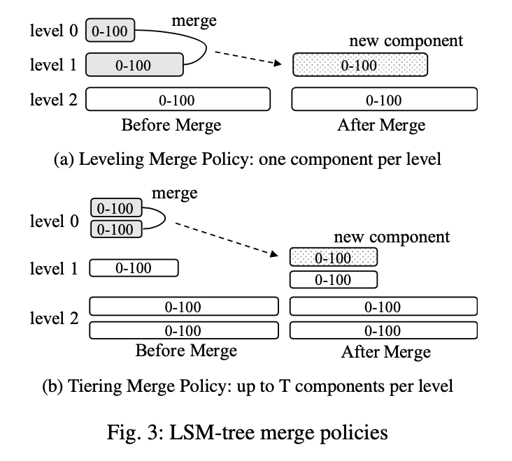
39BF2B48-BCF3-4DD1-9A39-C0FB3D042FEF

在介绍 compaction 之前，我们可以先介绍一下 sorted run: 每一层中，单个逻辑有序且不与其他重复的结构，比如 0-100, 会被视作一个 sorted run，这篇论文的用词是 component。

Leveling merge policy 会从 i 层单个 sorted run 中向 i + 1 层合并，成为 1 个 sorted run. 在 i 层的 key 平均要被 compaction 多次，才会 compaction 到下一层。

tiered compaction 则如下图所示，每一层会有可能不止一个 sorted run, 但只会合并一次：

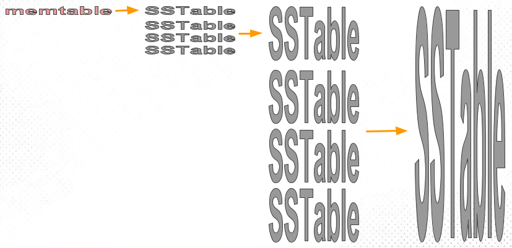
compaction-1

简单的说，leveled compaction 对读和空间放大有好处，tiered compaction 写放大比较少

常见优化

用 bloom filter 优化读

BF 优化读是一个很好的策略，这里就不再介绍 BF 了，但同时，需要注意的是，合并的时候可能要重新计算 BF，因为可能有些 tombstone 的数据，合并就给你不要了，所以 BF 这里有问题。

这里 Bloom Filter 很多时候只需要对应到磁盘上，所以经常是静态的（即不需要预先知道 key 的数量，来增插删改）。

此外，也有用 Cuckoo Filter 之类的方式，来在对应的需求下替换 BF.

partition

上面的 $C_i$ 不仅是逻辑的一层，也是物理的一整块结构。原始的 LSM-Tree rolling merge 只会把一部分叶子结点 merge 到一层。

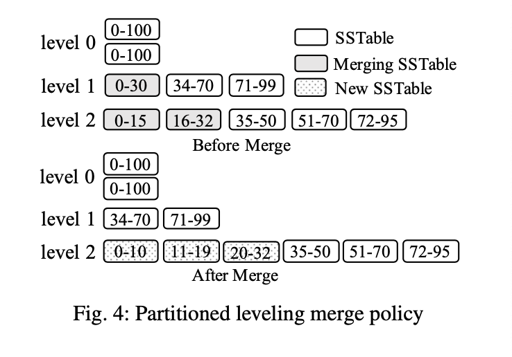
4ED4867F-2630-407D-9753-555D24D0D5C2

这里，LSM-Tree 可以把每一层 sorted run 分为多个 SSTable, 例如 LevelDB 默认使用 2M 左右的 SSTable.

这样的操作有下列的好处：

First, partitioning breaks a large com- ponent merge operation into multiple smaller ones, bound- ing the processing time of each merge operation as well as the temporary disk space needed to create new components. Moreover, partitioning can optimize for workloads with se- quentially created keys or skewed updates by only merging components with overlapping key ranges

上述是 Leveled compaction 的 partition，tiered compaction 需要一别的方式设计：

这里提供了一些方案：

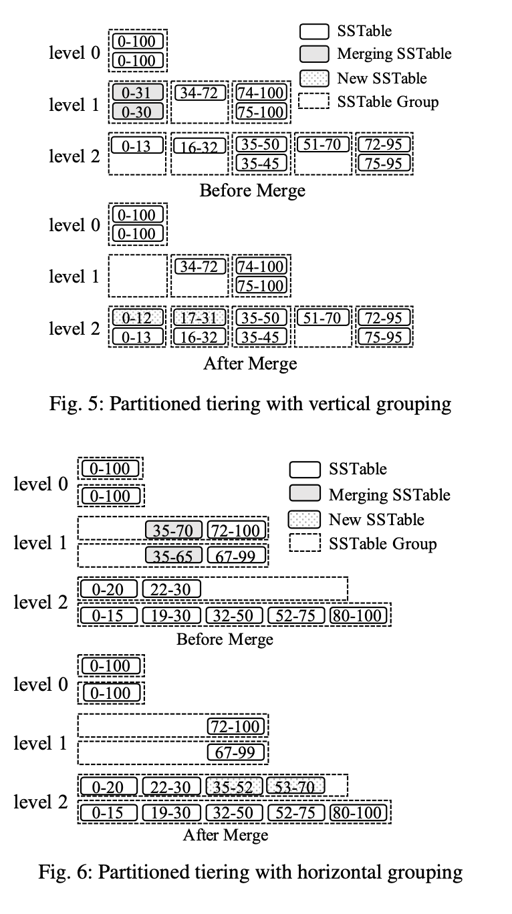
F3B0E1FA-89CD-4FFF-8D3A-0A33D1E0A811