Notes on Query Optimization

上一节我们介绍了 executor, 这节是优化器的入门。用户的 SQL 可以用某种关系代数的表达式表示。同时，我们可以利用关系代数推出某种等价性，两个关系表达式在所有可能的 db 集合都会产生相同元素集，那么这两个表达式是 等价(equivalent) 的。

上面我翻译的有点垃圾，贴下原文：

Two relational-algebra expressions are said to be equivalent if, on every legal data- base instance, the two expressions generate the same set of tuples. (Recall that a legal database instance is one that satisfies all the integrity constraints specified in the data- base schema.)

Note that the order of the tuples is irrelevant; the two expressions may generate the tuples in different orders, but would be considered equivalent as long as the set of tuples is the same.

DB 优化的过程需要：

  1. 生成与给定 expression 逻辑等价的表达式
  2. 产生不同的查询计划
  3. 估计每个 Plan 的开销，选择代价最小的

完成 (1) 需要有一些等价规则：

To implement the first step, the query optimizer must generate expressions equiv- alent to a given expression. It does so by means of equivalence rules that specify how to transform an expression into a logically equivalent one.

随即我们获得2，然后根据一些固定规则或者统计信息来进行优化。

Equivalent Rules 建议阅读原书，感觉我怎么讲都是把它们图贴一遍…总的来说，这些 rules 有下列的含义：

  • 关系代数有一些等价规则，我们希望，部分规则适用以后，产生等价于原始关系的结果，但产生较少中间关系
  • A set of equivalence rules is said to be minimal if no rule can be derived from any combination of the others.

此外，一些 Join 相关的，也能根据索引、公共属性等 Rules 来处理。

F86C9C0C-6F5F-4EB7-ACC7-9DD1DFA17AF9

上面的 genAllEquivalent(E) , 对于给定的 Expression E , 生成所有的等价表达式, 中间的部分阶段可以被称为 transformation。

等等，上面你肯定觉得太废了，实际上，我们可以减少开销：

  • E 和 E’ 可以在内存中共享一些表达式，感觉类似 COW-Tree 那样
  • 如果 Optimizer 在这个阶段分析 cost, 那么它能够减少很多不必要的生成。

Some query optimizers use equivalence rules in a heuristic manner. With such an approach, if the left-hand side of an equivalence rule matches a subtree in a query plan, the subtree is rewritten to match the right-hand side of the rule. This process is repeated till the query plan cannot be further rewritten. Rules must be carefully chosen such that the cost decreases when a rule is applied, and rewriting must eventually terminate. Although this approach can be implemented to execute quite fast, there is no guarantee that it will find the optimal plan.

上述描述的是 RBO 的概念，

Yet other query optimizers focus on join order selection, which is often a key factor in query cost. We discuss algorithms for join-order optimization in Section 16.4.1.

Estimating Statictics

一个操作的代价依赖于统计信息，例如：

  • 走不走某个索引？如果你要查的数据少的话，走索引能大大优化性能，但是你本身查询数据大，又要回表，那你就相当于白走一趟。
  • 走哪个索引？我们现在有很多索引，你要挑选可能比较少的一个来走。
  • Join 的顺序，我们怎么 Join 才能代价比较小

同时，我们不能先验知道所有数据，比如用户传了一个 a > 5 && a < 10, 那对应的行应该有多少呢？这个问题可能影响上述的决策。

数据库系统的 Catalog 可能包含下列信息：

  • $n_r$ , 包含 r 的 tuple 数目
  • $b_r$, r 相关的 tuple 数目
  • $l_r$ ，关系 r 中每个 tuple 包含的 bytes
  • $f_r$, 一个磁盘块能容纳 r 中 tuple 的个数
  • $V(A, r)$, 关系 r 中属性 A 的非重复值个数。

索引相关的，比如 B+Tree 的信息，或者有没有索引，可能也可以维护在 Catalog 中。

此外，db 可以维护一个 histogram:

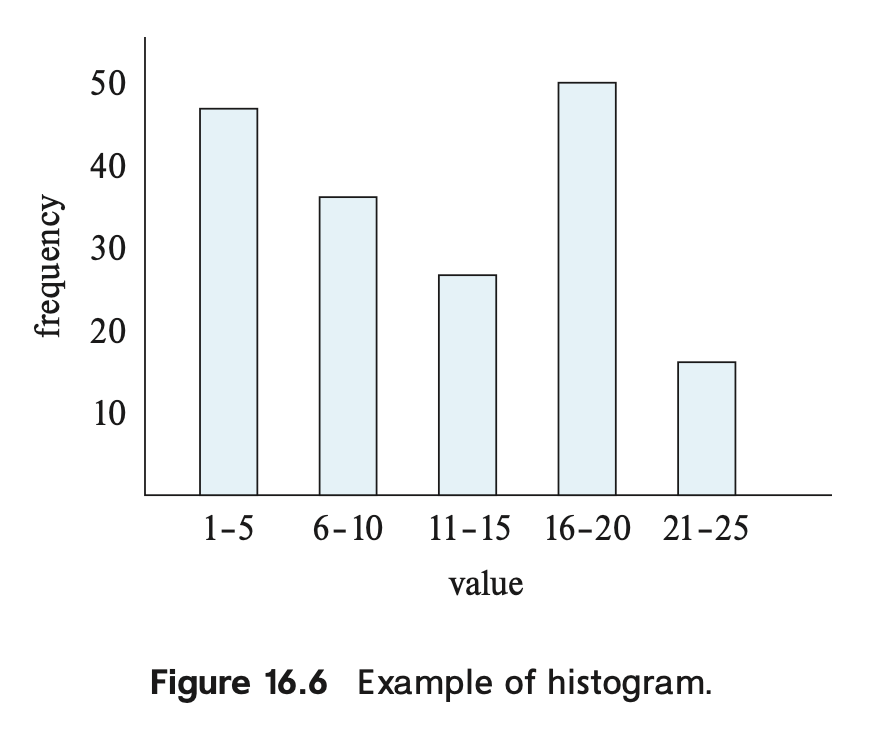
3CDD7A79-37C8-4B1E-8CA5-2B55F8E8587B

通过直方图，来表示细粒度区间的取值。否则，db 可能会只保存最大值和最小值，然后假设数据分布是均匀的。

那么，我们有以上信息之后，可以做一些基本的估计：

  • $\sigma_{A=v}(r)$ 均匀分布的情况下，可选有 $n_r / V(A, r)$ 个 tuple, 如果有直方图的话，可以在直方图对应取值定位。
  • $\sigma_{A<v}(r)$ 等同理
  • Conjunction/Disjunction 中，假设个条件独立，有下列计算方式：
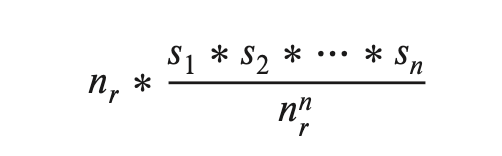
    513E6593-9478-41F7-A551-5315F009DA2F
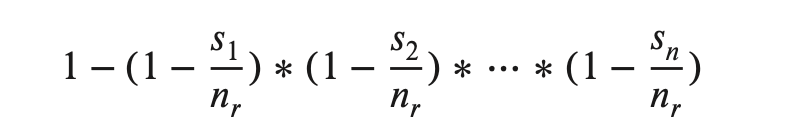
    304D1058-66C2-45B4-8A84-5AE5AF25CFA5

特别地指出，有一些特殊的高频值，可以被特殊的单独记录到一个高频值集合中。然后这些值的估计可以走这个单独的几何，来防止这些特殊值影响统计。

Join size Estimation

  • 笛卡尔积大小就是 * 一下得了，反而最简单，$r \times s$ 就可以了，产生结果每个 tuple 大小 $l_r + l_s$

估计自然连接的大小会复杂很多：

  • $R \cap S = \emptyset $ ，退化为笛卡尔积的计算方式
  • 如果 join 的是 R 的 key, 那元素至多不会多于 S。这个可以用 $V(A, s)$ 来做一个估计：
    • 对一个 R 中的 tuple t，可能会与 $n_s / V(A, s)$ 的产生连接
    • 所以总共 $(n_r * n_s) / V(A, s)$ 组
    • 但是上面是在各个概率相等的情况下出现的，实际上可能需要更复杂的区间统计。同时另一种算法会给出 $(n_r * n_s) / V(A, r)$, 一般取小的

其他估计

FCC0B444-CCC3-4E26-9767-2A887566FBBB

查询结果的分析

假如我们需要 $V(A, \sigma_{\theta}(r))$, 那我们要对他内部分析：

  1. 可以取它为 A 等于单个值，或者 A 等于一个集合
  2. 可以乘以一个系数 $V(A, r) * s$, s 为系数
  3. 可以用一些更精确的概率来分析

假如我们要估计 Join 的结果：

68AFA23D-75CC-4247-9468-5E944A08F7CF

简单来说，看 Join 条件是独立的，跟A有关，跟B有关，还是都有关，然后根据概率来估计

信息收集

如果每个 Update 都收集统计信息就太废了。一来系统有 HLL 这些模糊方式，和采样，二来系统可以在一段时间后手动 analyze 或者自动重建统计信息。

MySQL 的 InnoDB 中，有一个 innodb_table_stats 表，大概内容如下：

它的配置可以参考：https://dev.mysql.com/doc/refman/5.7/en/innodb-performance-optimizer-statistics.html

大概信息如：

Field Type Null Key Default Description
database_name varchar(64) NO PRI NULL Database name.
table_name varchar(64) NO PRI NULL Table, partition or subpartition name.
last_update timestamp NO current_timestamp() Time that this row was last updated.
n_rows bigint(20) unsigned NO NULL Number of rows in the table.
clustered_index_size bigint(20) unsigned NO NULL Size, in pages, of the primary index.
sum_of_other_index_sizes bigint(20) unsigned NO NULL Size, in pages, of non-primary indexes.