事务:协议和隔离

事务：隔离级别和协议

应用程序员会依赖事务这么一种抽象：事务。它提供了 ACID 的抽象，A 可以理解为多行数据读/写的原子性；C 据说是用来凑数的；I 表示事务中间有某种互相隔离；D 表示事务是持久的。对于应用程序员而言，抽象是隔离级别。关于这点，可以简单这么理解：隔离级别越高，冲突越剧烈，可能的性能会更差。而我们也可以牺牲一些保证，来提供性能

对应用程序员而言，需要理解的是隔离级别，甚至数据库更上层的建模、缓存。ANSI-92 中给出了一定的隔离级别的定义，但是对乐观的事务而言，我们仍然需要理解一些不同的标准。我们下面会介绍一些隔离级别，这里援引了 DDIA 的定义：

  1. Read Committed:
    1. （最基础的隔离级别，很多时候
    2. 从 DB 读的时候，只能看到已经提交的数据，没有脏读
    3. 写入的时候，不会覆盖掉未写入的数据，没有脏写
    4. 可能的实现：行级别的 Lock，或者是 MVCC/COW 等机制
  2. Repeatable Read: 没有 read skew
  3. Snapshot Isolation: 从一个一致性的视图中读取
    1. 没有read skew
    2. 可能会有 write skew
  4. Serializable: 所有事务的调度是可串行化的

我们还有一些现象，代表某种程度上对事务的 break：

  1. Dirty reads: 看到了未提交的数据
  2. Dirty write: 不能覆盖另一个事务的尚未提交的一部分
  3. Read skew/unrepeatable read: 两次读同一个 record 可能读到不同的值
  4. write skew: 可以将写入偏差视为丢失更新问题的一般化。如果两个事务读取相同的对象，然后更新其中 一些对象（不同的事务可能更新不同的对象），则可能发生写入偏差。在多个事务更新同一
    个对象的特殊情况下，就会发生脏写或丢失更新（取决于时机）。在 PG MySQL/InnoDB 等的 RR 级别下，都无法避免 Write Skew
  5. phantom read：DDIA 认为这是导致写入偏差的根源，SELECT 查询到符合条件的 columns，然后按照条件操作一个 subset。这个时候，一个事务中的写入导致了另一个事务查询结果被改变。

其实上面这些我整理的还是挺乱的，有空的可以回顾一下 DDIA…但是上面这些虽然乱，但是对应的内容其实是不难懂的。难就难在显示可能有点区别：

  • DDIA 的定义倾向于 2PL + MVCC 相关，但是实际上会有不同的实现。别看实现都会尽量实现标准，但是在数据库领域，某个地方的实现能决定太多的行为了。
  • 有很多数据库采取乐观的并发控制，他们的表现会不会不太一样？
  • 有部分数据库实现上采取 SI 代替 RR，这会不会导致定义上有什么问题？
  • 如何理解 MySQL，PG 这类的隔离级别？
  • “写后读” 这些定义和上述有什么关系？

我们尽量以不介绍实现的情况下来讲讲，但是下面内容可能不可避免的要求你对 2PL MVCC SI 有着最基础的理解。在数据库领域，某个地方的实现能决定整个链路的行为。

ANSI-92 Phenomena

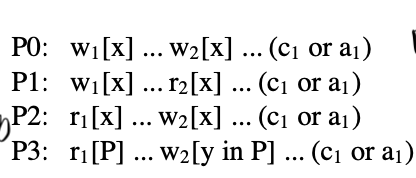
8A4D7051-23D4-43B1-9E29-90FC938CD97A

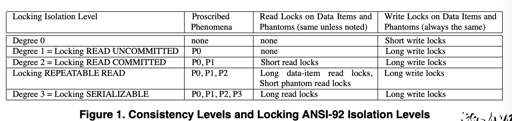
6B34260B-EF80-4FA3-AC86-94F2B91FD159

1/2 表示事务 ID，c a 表示 COMMIT ABORT，那么我们可以很好的把上面的四个 P 对应到 DDIA 的定义中。这个需要放到单对象 + Lock 的环境下理解：

  1. P0: 对单对象的覆盖写入，即脏写，导致仅 COMMIT 的时候数据库的状态为 Txn2 的写入。
  2. P1 对单对象的脏读。如果 TXN1 abort 了，那么显然很危险。
  3. P2: 写修改了读, 类似不可重复读的修改。
  4. P3: Phantom Read，对于某个 Predicate 的读 — 改

懂了这些，你应该很好看懂上面的定义。

但是你可以发现，其实某些时候，在乐观并发或者 MVCC 下，有些调度甚至是没问题的。SI 甚至让事情更模糊。这里我们可以参考另一篇论文，《Generalize Isolation Level Definitions》的定义了。

懂了这些，你应该很好看懂上面我们在第一节的定义。但是这个定义是又麻烦的：对于乐观甚至 MVCC 的实现，我没可能不会显示锁定/允许读写是并存的，那么这个定义实际上就是不能满足的。实际上我们可以 break P0/P1：

1
H1: r1(x, 5) w1(x, 1) r1(y, 5) w1(y, 9) r2(x, 1) r2(y, 9) c1 c2

那么，这里 break 了上面的要求，但是仍然是可串行化的调度。所以我们需要一个更 specific 的模型来描述。

建模: History Event Order

我们需要确切描述事务，我们就需要一个具体的模型。我们先远离关系的概念，从 row/tuple 开始：

  • row/tuple 是一个 object，对于单个 Object 而言，事务以一个 total order 操作这个 object

  • 一个 object 有 1 个以上的版本，可以读到 committed, uncommitted 甚至 abort 的数据

  • 如果 $T_i$ commit 了，那么认为对 $T_i$ 而言，它写入的任何一个 Object 的版本 $x_i$ , $T_i$ install $x_i$, 如果 $T_i$ abort 了，那么 $x_i$ 不会被视作 committed 的一部分。

  • $T{init}$ 是一个抽象的事务，它被视作最初的事务，给每个出现的 object 一个虚拟的初始版本 $X{init}$ ，当事务第一次写入的时候，从 init 变成最初状态。当这个 object 被删除的时候，被标记成最终版本 $X_{dead}$ 。

  • 如果一个对象被删除后又被插入了，那么视为两个不同的对象。

我们把整个操作的序列称为 Transaction History，History 有两部分组成：

  • 偏序的 Events (E)
  • 全序的 version order

Event

对于 Event，我们可以有：

  1. Read(r)
  2. Write(w)
  3. commit(c)
  4. abort(a)

我们有如下的记号

  1. TXN j 读 X 读到版本 i, 获得值 v，可以记作 $rj(x_i, v)$ 或者 $r_j(x{i.v})$
  2. TXN i 写 X 写入到版本 i, 值 v，可以记作 $wi(x_i, v)$ 或者 $w_i(x{i.v})$

对于这个 order，我们要明白 Event 和 version order 的规则：

对于 Event 而言，它保证了事务的偏序关系：

  1. 如果 $rj(x_i, v)$ 存在，那么它 preceded by $w_i(x{i.v})$, 并且对应着“最近的写入”
  2. 在 Event 中，如果 $wi(x{i.v})$ 和 $rj(x.m)$ 中没有任何一个 $w_i(x{i.{v2}})$, 那么 $rj(x.m)$ 独到的必定等于 $x{i.v}$
  3. History 必须是完整的，有事务就必须有对应的 commit/abort

Version

对于 version 而言：

  1. 对象 x 有一个 init 版本和至多一个 dead 版本
  2. 它的可见版本在 init 版本和 dead 版本之间
  3. 如果 History 有 $r_j(x_i)$ 那么 $x_i$ 为可见版本，无论是否 commit

同时，需要注意的是，version order 不一定和写入顺序是完全一样的：

1
2
w1(x1) w2(x2) w2(y2) c1 c2
r3(x1) w3(x3) w4(y4) a4

这里 x2 在 x1 后写入，但是因为 commit 的 order，实际上对应的 x1 在 x2 前。

Predicate

对于谓词而言，我们需要引入额外的记号。P 是一个 Boolean expression，在数据集里面，满足这个要求的版本集合被称为 Vset(P) 。注意，这个集合 之包含存在的记录，未涉及的 init 记录这些是不存在的, 它只包含对应的 visible 对象。

对于读取而言，假设有下列的 SQL：

1
SELECT * FROM EMPLOYEE WHERE DEPT = SALES;

同时有 x, y 两个 object ，它们的版本分别为 1 2，x 满足 DEPT=SALES满足需求的 z0 在未来会被插入。

那么我们需要写出对应的：

1
rj(P: Vset(P)) rj(xj) rj(yj) ...

对，这下复杂了很多：

1
ri(dept=sales: x1; y2) rj(xj)

Dependencies

这篇论文定义了三种 conflict，同时分为了 regular conflict 和 predicate-based conflict。它们描述的是事务之间的依赖关系。

Read Dependencies

predicate-based conflict

对于一个 Predicate，如果某个事务在它读之前，插入了满足 Predicate 的记录，那么会有 read dependency

Directly Read Dependency

事务 $T_j$ direct read depend $T_i$ 时，会有下列的条件：

  • directly item-read-depents: Tj 读到了 Ti 写入的记录
  • directly predicate-read-depends: Ti 更新了满足匹配 Vset(P) 的对象，并且被 Tj 读到了

Anti Dependency

当事务覆盖了另一个事务独到的值的时候，产生了 anti-dependency。

predicate-based conflict

对于一个 Predicate，如果某个事务在它读之后，插入了满足 Predicate 的记录，那么会有 anti dependency

Directly Anti Dependency

事务 $T_j$ direct anti depend $T_i$ 时，会有下列的条件：

  • directly item-anti-depents: Ti 覆盖了 Tj 读到的记录
  • directly predicate-anti-depends: Ti 更新了满足匹配 Vset(P) 的对象，他之前并且被 Tj 读到了

Write Dependency

如果事务 $T_i$ 覆盖了 $T_j$ 写入的版本，那么它们有 direct-write-depend。

Serialization Graph

9702A3CB-D18C-4751-AF2E-4B346C879B2F

有一点关键是，事务或许不是全序的，但是至少应该是偏序的。所以，我们对事务构建 DAG，不应该存在环。

那么，通过上述几种 dependency，我们可以构建依赖的有向图，来判断具体的关系。

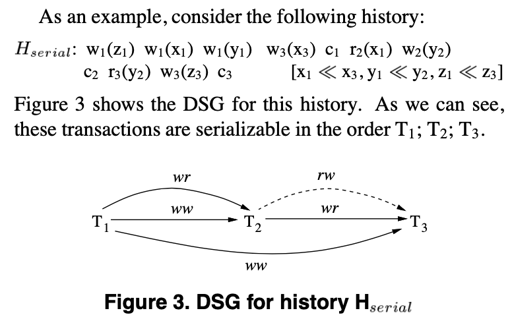
53878744-E179-4603-B768-D80DBCFD58EF

同时可以定义 depends 关系：

33241D20-8EB6-46C6-9AAD-EDAC95237199

New Generalized Isolation Specifications

Like the previous approaches, we will define each iso- lation level in terms of phenomena that must be avoided at each level. Our phenomena are prefixed by “G” to denote the fact that they are general enough to allow locking and op- timistic implementations; these phenomena are named G0, G1, and so on (by analogy with P0, P1, etc of [6]). We will refer to the new levels as PL levels (where PL stands for “portable level”) to avoid the possible confusion with the degrees of isolation given in [8, 13].

这里用 G 表示 phenomena，PL 表示 portable levels。

PL-1

这个对应的其实相当于 P0，我们抄英文看看原定义：

we define PL-1 as the level in which G0 is disallowed:

G0: Write Cycles. A history H exhibits phenomenon G0 if DSG(H) contains a directed cycle consisting entirely of write-dependency edges.

89DEB4D5-C31F-4430-9C08-B1E314CAF4A6

实际上覆盖写未提交的本身在 2PL 意外的实现中不一定出了大问题，但是如果有上述的重复覆盖，那么就会真正出现问题。即如上图。同时论文也给出了 predicate 相关的 $H_{wcycle}$

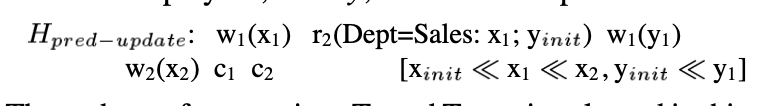
813DDC98-A805-41A7-B406-9D4986272255

PL-2

PL-1 对读是没有限制的，当然，出现我们之前说的“脏读”就太正常了。

G1 由 G1a G1b G1c 构成：

DF4CBE7C-03E6-4F03-83A2-5DD32CB18F17

G1a: 读到了 abort 事务的数据。

8F504CF7-0381-4DBB-810E-65126DE2D4A8

G1b: 读到了事务中间 的数据

FC512948-7B2A-4A46-BFA8-BABC63264652

G1c: 产生了 direct 的环。即 direct rr, rw, wr 的环。

Phenomenon G1 captures the essence of no-dirty-reads and is comprised of G1a, G1b and G1c. We define isolation level PL-2 as one in which phenomenon G1 is disallowed. Proscribing G1 is clearly weaker than proscribing P1 since G1 allows reads from uncommitted transactions.

实际上，这个相当于 read committed, 但是会弱一些：

Proscribing G1 is clearly weaker than proscribing P1 since G1 allows reads from uncommitted transactions.

P1 不允许脏读，那么 PL-2 靠：

  1. 不允许读到 abort/中间的数据，但是允许短暂读到 uncommitted 的数据

实际上，这相当于，被 committed 的事务 可以读到 未提交但未来被提交 的数据。

direct 依赖的环比较难理解，就是 Figure2 那些。这个我简单推导一下为什么这个能满足 对应的 read committed：

  • $T_i$ 事务读一组 x, y, z… 读到 $x_k$ $y_k$ …
  • $T_i$ 在一组子集上再次读，读到了 $T_j$ 写入的数据，这个时候，$T_i$ depend $T_j$
  • $T_j$ 如果有任何情况下直接依赖了 $T_i$ 的数据，那么这个顺序就被 break

但是这个没有禁止 anti-dependency, 即 P2 P3 对应的

  • $T_j$ $T_k$ 事务读一组 x, y, z… 读到 $x_k$ $y_k$ …
  • $T_j$ 修改了 $x_k$ ，改为 $x_j$ , commit, 这个时候 $T_k$ anti depend $T_j$
  • $T_k$ 读到了 $x_k$ , 这个时候 $T_j$ depent $T_k$

好了，break 了！

PL-3

60CD6506-2D23-46AC-AAC2-655921CADD0C

禁止所有 anti-dependency 之后，整个事务就变的有序了。这对应 serializable。其实这个相对来说是最好理解的。

PL-2.99

这个对应的是 repeatable read.

5E61590D-1A6F-4C8D-9E8A-1E542DEE85E7

它允许 Item Anti-dependency, 用来处理可重复读。

Snapshot Isolation: PL-SI

我一下没找到这个定义，有点蒙圈，后来发现在博士论文 4.3 里…

好吧，坑啊！这里定义了 PL-2+ 来引入 PL-SI：

PL-2+

PL-2+ 表示看到一致性视图的最低级别

G-single: Single Anti-dependency Cycles. A history H exhibits phenomenon G- single if DSG(H) contains a directed cycle with exactly one anti-dependency edge.

Level PL-2+ proscribes G1 and G-single. Intuitively, PL-2+ provides consistency because cycles with one anti-dependency edge occur exactly when some transaction both observes and misses modifications of another transaction.

PL-2L

这个级别表示了单调读。

PL-SI

02E27F7E-B745-41F5-81F0-52A2D284F9D1

具体定义还是蛮复杂的，简单来说是：

  1. 涉及一个 start 的时间戳的序，在 start 开始之后的 read-write dependency 不能存在（但是可以存在 anti-dependency, 如下文所述）
  2. 写入不发生冲突
  3. 允许 PL-2+ 定义的 consistent view, 可以有且仅有单个 anti-dependency 边的 cycle 存在。（

现实中的数据库

https://github.com/ept/hermitage

上面这个链接是现实数据库中对应的隔离级别。